[文章摘要]：本人半年前在由中国科学院主办、中国科学技术协会协办的“科学智慧火花”上连续发表了六篇讨论磁力本质的的文章，在这些文章中明确指出：磁力只是多电荷在不同运动状态下产生的库仑力的矢量叠加结果。本文基于此观点提出了真空磁导率的理论值的计算方法，并在此基础上得出了简化计算结果约为8k/C²，比实测值的2πk/C²稍大一些，但还是很令人振奋的。相信通过精确计算，能得到更加接近实测值的结果的。希望得到国内外专家、学者和物理爱好者的支持与帮助。

一、真空磁导率的精确计算方法简述

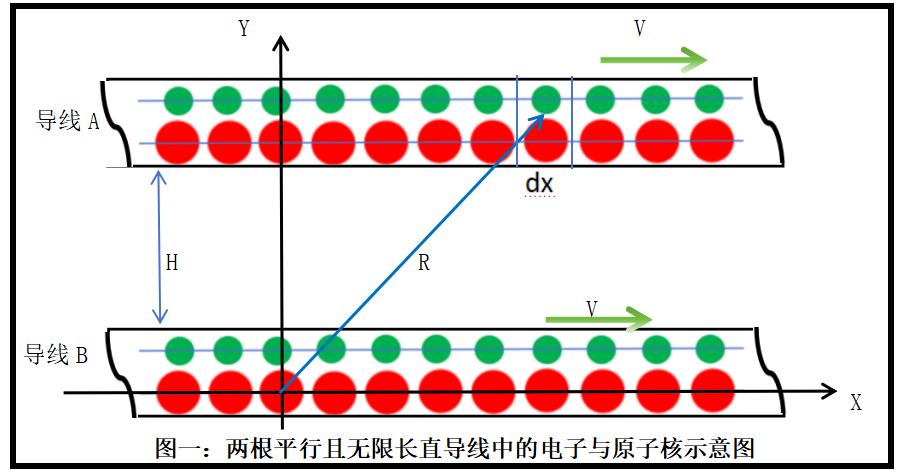
基于本人在已发表的六篇论述磁力的本质文章中的论述，我们有理由认为：磁力只是多电荷在不同运动状态下的库仑力的矢量叠加结果。因此，真空磁导率应该是两根相距1米的无限长平行直导线中参与电流的运动电荷及其对应的离子/原子核之间才存在的库仑力的矢量叠加结果。如下图一所示：当图中的H=1米时，假设导线A中参与宏观电流的运动电子与导线B中参与宏观电流的运动电子间的库仑力为F₁、导线A中参与电流运动电子所对应的离子/原子核与导线B中参与电流运动电子所对应的离子/原子核间的库仑力为F₂、导线A中参与电流的运动电子与导线B中参与电流运动电子所对应的离子/原子核间的库仑力为F₃、导线A中参与电流运动电子所对应的离子/原子核与导线B中参与电流的运动电子间的库仑力为F₄的话，则真空磁导率为：μ_理论值=F₁+F₂+F₃+F₄。

    1、相对运动电荷之间的库仑力计算方法简述

库仑定律是描述两个相对静止的带电体之间存在的相互作用力，即库仑力。但如果两个带电体是相对运动的，则因为库仑力的相互作用速度不是无限大的，而是有限的实际情况，且相对静止时相互作用速度为U的话，相向运动时则为U+V，反之为U-V。所以，库仑定律不再完全适用，需要进行适当的修正。

由于带电粒子的相对运动和库仑力相互作用速度有限，可能导致带电粒子之间任意时刻的库仑力与静止时不同：任意特定时刻的库仑力是较早一些时刻的实际距离时的库仑力。当带电粒子相互远离时，库仑力会大些，反之就会小些。

1.1、相对远离的带电粒子间的库仑定律修正

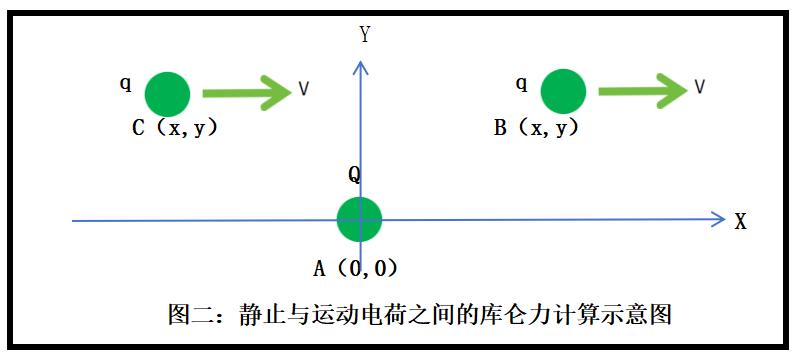
如上图二所示：当位于B点的带电粒子以速度V沿X轴正向运动时，任意特定时刻t时，带电粒子B与位于坐标原点静止的带电粒子间的库仑力为更早一些时刻t'时的距离R'上产生的库仑力。令△t=t-t',则有：

上式中的

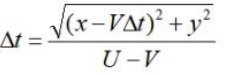
则有：

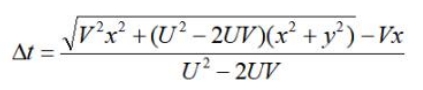
1.2、相对靠近的带电粒子间的库仑定律修正

如上图二所示：当位于C点的带电粒子以速度V沿X轴正向运动时，任意特定时刻t时，

带电粒子C与位于坐标原点静止的带电粒子间的库仑力为更早一些时刻t时的距离R上产生

的库仑力。令△t=t-t’，则有：

上式中的

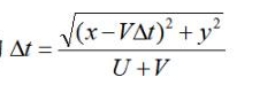
则有：

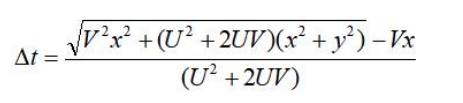
2、真空磁导率计算公式

2.1、根据真空磁导率的定义，两根处于真空中的无限长且相互平行的直导线，它们的间距为H=1m，每根导线中的电流强度为1安培且电流方向相同。两根导线相对静止，且导线中形成电流的电子的运动速度均为V，单位长度内的、参与电流的移动电子数量及其对应的离子/原子核均为N。

2.2、两根无限长导线间四个分力的计算

由于导线A为无限长，其对导线B中的电荷产生的库仑力只有Y轴方向的分量，沿X轴方向的库仑力分量为0。因此，F₁、F₂、F₃、F₄四个分力的方向均是沿Y轴（垂直导线）方向的，并且正值为沿Y轴的力，负值为与Y轴相反方向的力。

2.2.1、导线A中所有参与电流的电子与导线B中位于坐标原点上的电子间的库仑力

由于导线A和导线B中的电流大小和方向相同，因此，两根导线中的参与电流的电子的运动速度的大小与方向也相同，也就是它们之间是相对静止的。可以直接应用库仑定律。

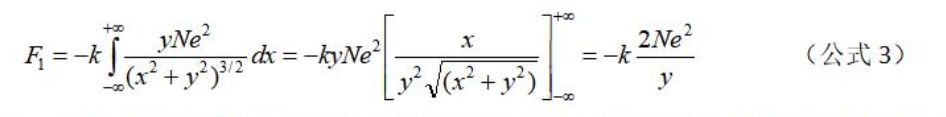
3.2.2、导线A中所有参与电流的电子所对应的离子与导线B中位于坐标原点上的离子间的库仑力由于导线中的所有离子相对导线静止，因此，两根导线中的离子都是相对静止的，可以直接应用库仑力。因离子所带的电荷量等于其对应的电子，只是电性相反。因此有：F2-F，既：

3.2.3、导线A中所有参与电流的电子与导线B中位于坐标原点上的离子间的库仑力根据（公式1）及单位长度的参与电流的电子数量为N以及合力仅沿v轴方向，则有：

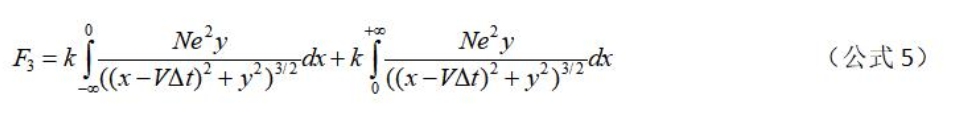
3.2.4、导线A中所有参与电流的电子所对应的离子与导线B中位于坐标原点上的电子间的库仑力根据运动的相对性可知：F=F，即有：

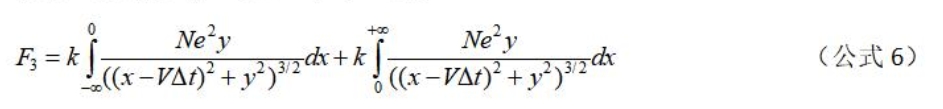
3.2.5、导线B中的单个参与电流的电子及其对应的离子受到导线A中的所有参与电流的电子及其对应的离子之间的库仑力之和F为：

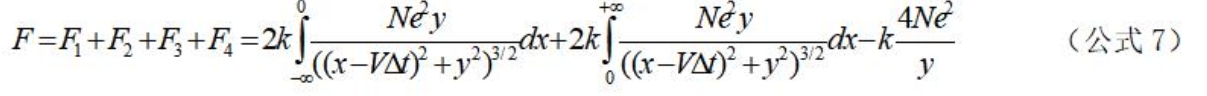
3.2.6、导线B单位长度受到导线A中参与电流的电子及其对应的离子的库仑力（公式7）是导线B中参与电流的单个电子及其对应的离子受到导线A中所有参与电流的

电子及其对应的离子之间的库仑力总和，而导线B单位长度受到的力是该力的N倍。因此有：

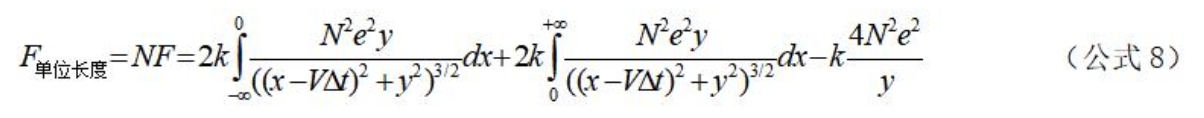
3.3、真空磁导率理论计算公式

将以上（公式8）中的y修改为1，则（公式8）的计算结果就是真空磁导率理论值，即：

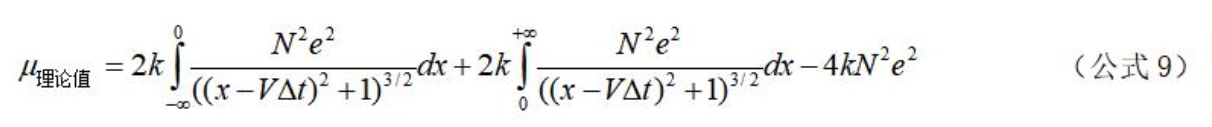
二、真空磁导率理论值的近似计算

1、近似计算的假设条件与计算过程

由于（公式9）中的△t与库仑力相互作用速度U、带电粒子的相对运动速度V以及带电粒子的实时位置（x,y）等相关，直接利用该公式计算真空磁导率理论值难度太大。因此，本文拟简化计算过程，其计算结果可能与真值存在一定的差异，但应该可作进一步的研究之参考。

已经：当x<0时，

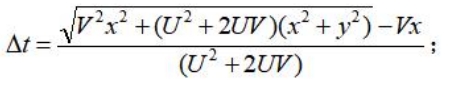
当x>0时，

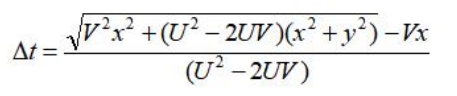
且y=1

为了简化计算，我们假设y=0，则有：

当x<0时，

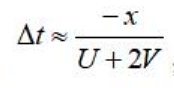
当x>0时，

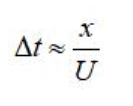
带入（公式9）并整理可得：

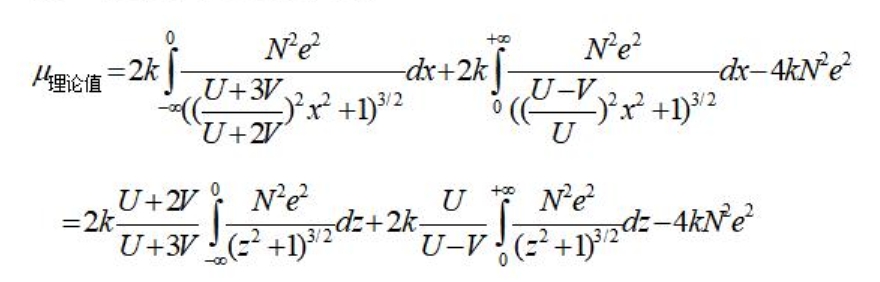
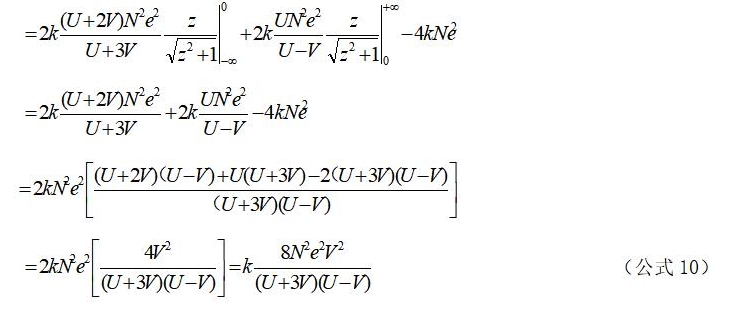
2、电流为1安培时，参与电流的电子单位长度内的数量N与其运动速度V存在如下关系：

3、真空磁导率的理论计算值与实测值的比较

已知真空磁导率实际值与库仑常数间存在如下关系：

比较（公式11）与（公式12）可知：如果真空中库仑力的相互作用速度为真空中静止光源产生的光之速度C，参与电流的电子在导体内的运动速度V的影响忽略（V=0），则理论值与实测值仍存在较大差异，但并不存在根本性差异。理论值大概是实测值的127.32%。

如果要使理论值与实际值相吻合，则在假设库仑力相互作用速度为真空中静止光源光速的情况下，参与电流的电子的运动速度V=？

假设V=mC，m介于0~1之间，则（公式11）可修改为：

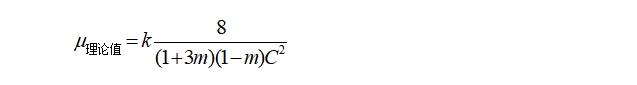
因此，当8/[（1+3m）（1-m）]=2π时，则真空磁导率理论值等于实测值。因此有：

         3m²-2m+（4-π）/π=0

上式的两个解为：

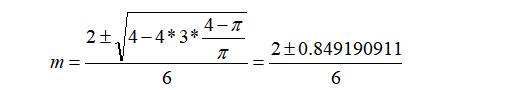
则有：m=0.191801515  或m=0.474865152

也就是说：当V=0.191801515C或0.474865152C时，真空磁导率理论值就与实测值相同了。

4、真空磁导率理论计算值与实测值存在差异的可能原因

真空磁导率理论计算值与实测值存在差异的主要原因可能有三：

4.1、计算真空磁导率理论值时用的是导体中电子相对导体本身运动的真速度，而不是视速度。由于两根导线间存在1米的距离，视速度与真速度在x绝对值较小的区段内的差异还是很明显的，且这区段对总的理论计算值的影响更大些。由此导致理论计算值与实测值存在一定差异也是正常的。

4.2、真空中两个带电粒子间的库仑力相互作用速度可能并非正好等于真空中静止光源产生的光之速度，从而导致理论计算值与实测值存在偏差。

4.3、真空磁导率实测值并不是在理想的真空环境下用两根无限长平行导线测得的。也就是真空磁导率的实测值本身也存在较大误差。

二、真空磁导率理论计算的物理意义

通过以上对真空磁导率的理论计算，虽然计算结果与实测值存在一定的偏差，但两者还是比较接近的。不仅从力的方向上一致，力的大小上也不存在根本性差异。因此，本文提出的计算真空磁导率理论值的方案还是有其巨大价值的。这不仅揭示了真空磁导率与光速及库仑常数之间存在的内在关系，也明确了磁力就是特殊条件下的库仑力的事实，从根本上否定了磁力是独立于库仑力的另一种力的观点。

另一方面，可能也预示着所谓的光速应该与光源的运动状态有关。这也是库仑力相互作用速度与带电粒子的运动状态有关的根本原因所在。