临界点附近物质所呈现的特殊的性质,称之为临界现象。如何准确描述临界现象?在扼要温故之后，应用分别描述饱和蒸气与液体的玻尔兹曼因子方程，准确描述气液相变的临界点特性。

1.温故

1.1范德瓦尔斯方程

1.1.1临界系数K_k

由范德瓦尔斯方程中的常量a与b可以确定临界点K_k的状态参量^[1]：

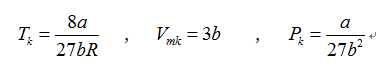
由上列状态参量可以得到临界系数K_k

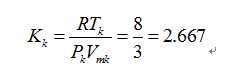
也就是说，根据范德瓦尔斯方程，临界系数K_k对于一切物质都相同,是一个普适常量。但实际上，不同物质的临界系数K_k具有不同的值，而且与2.667相差甚大。所以，“范氏理论在定量上还不能正确地描述临界点附近气体的性质^[2]”。

1.1.2对应态定理

由状态参量与临界点状态参量的比值代入范德瓦尔斯方程中，可以得到对比物态方程。根据对比物态方程，两种气体的对比温度θ=T/Tc、对比压强ω=P/Pc、对比体积φ=V/Vc，三个量中只要两个相同，第三个也必然相同。这就是气体的对应态定律。

“实验证明，只有对于化学性质相似而临界温度相差也不很大的物质，对应态定理才具有很高的精确度，一般情况下，与实际情形是偏离的^[1]。”

1.1.3临界指数

通常引入具有普适性的临界指数(与物质的个体无关，即与范氏方程中的a和b无关)：定容比热容指数α、密度与温度关系指数β、等温压缩系数指数γ、压强与密度指数δ等，来讨论临界点附近热力学量的性质。

“范氏方程给出的临界指数定量不准确^[3].……为了对体系在临界点附近性质作出正确的描述，还须要建立新的理论。^[2]”

1.2朗道的有序相变理论

1937年，前苏联物理学家朗道发表的有序相变理论，是一种十分成功的唯象理论。它的核心是将热力学势在临界点附近展开为所谓的“序参量”的幂级数。

“朗道理论是一种普适的平均场理论，反映了各类不同相变的本质联系。但是，这个理论毕竞是唯象理论，有较大的局限性。由表10.3看出，它所得到的临界指数的值，与实验结果仍有很大的偏离^[2]。”

1.3 K.威尔逊的重正化群变换理论

“1971年，K.威尔逊把重正化群的方法用于统计物理学中临界现象的研究，建立起二级相变理论”。他的理论“不是正面处理，而是把问题分解成一系列简单得多的问题”。“他的分析证明，当足够趋近临界点时，系统的大多数变量都成为多余的。临界现象基本上决定于两个数：系统的尺度和所谓的量级参数”。他“全面阐述了物质接近于临界点的变化情况，还提供了这些临界量的数值计算方法”。“K.威尔逊的理论从基本原理上给出了一个有说服力的证明。计算所得的临界指数和实验结果相符合得很好。”

所谓“对于古老的气液相变,我们今天的知识并不比范德瓦耳斯增加了很多.……只有在临界点附近，我们的理论认识才大为前进了。^[3]”，说的就是朗道与K.威尔逊的相变理论及其对临界指数的数值计算。必须指出，朗道与K.威尔逊的相变理论并未解决“统计物理学处理互作用粒子系统所遇到的困难^[4]。”问题，其局限性是必然的，也是本质性的。

2.知新

应用玻尔兹曼因子方法，可以推导出分别描述饱和蒸气与液体平衡体系的纯理论的玻尔兹曼因子方程方程[5]；进一步可以导出气体、液体平衡体系的表面热力学函数、摩尔气体定压热容与定容热容之差、液体气化热、沸点气化熵、表面张力系数及其温度变化率、冰的升华热等一系列物质特性参量的理论公式;不仅对氢、氮、水、水银等物质多项特性参量进行定量计算的理论结果与实验观测值高度吻合[5],而且实现了用简洁的数学语言精确描述物质的临界点特性。

2.1气体临界系数Kk的精确描述

由于在临界点上液体的摩尔体积V_{i m}与饱和蒸汽的摩尔体积V_qm相同,等于临界摩尔体积V_qmc,故描述摩尔气体的玻尔兹曼因子方程变为^[5]

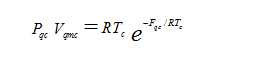
上式表明，气体的临界系数K_k可以用临界玻尔兹曼因子e^-Fqc/RTc 的倒数精确描述，即

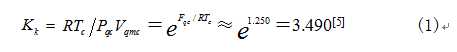
式1就是精确描述气体临界系数K_k的数学表达式与各种气体公共的近似值3.490。

式1表明： 临界系数K_k的精确值取决于F_qc /RT_c的大小，而F_qc取决于临界点时气体分子平均间距(即气体的摩尔体积)的大小(微观上与分子之间相互作用合力相对应)。

2.2  气体临界系数的趋同特性

对《气体数据手册^[6]》中所列156种气体（除空气外，其余155种均为单一纯气体产品）进行实例计算分析,结果表明：公共临界系数3.490相对于156种气体临界系数的实验观测值，相对误差小于5%的气体有81种,小于10%的有124种，小于20%的有147种，分别占气体总数（156）的51.92%、79.49%与94.23%。相对误差大于20%的气体只有9种，只占气体总数的5.77%.这一事实有力地说明了，实际气体的临界系数虽然不符合范氏理论的“普适常量”论断，但确实存在趋同的特性.也就是说，若将临界玻耳兹曼因子指数- F_q/RT确定为经验常量-1.25，则在20%误差范围之内，有94.23%的各种类型气体的临界系数都可以近似认为是相同的，近似为公共临界系数3.490. 更确切地说, 是临界玻耳兹曼因子e^-Fqc/RTc的趋同性,决定了临界系数K_k的趋同性^[5]。

应用气体临界玻耳兹曼因子e^-Fqc/RTc的趋同性，解析各种类型气体临界系数K_k的趋同特性，明显比范氏普适常量2.667更加准确，物理意义也更加明晰。

2.3  临界点上表面张力系数等于零

由单元液体的玻尔兹曼因子方程可以推导出液体表面张力系数的理论公式[5]

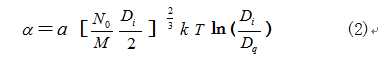
式2表明，液体表面张力系数α是温度T 、液体密度D_i与饱和蒸气的密度D_q的函数。由于临界点上“液体及其饱和蒸气间的一切差别都消失了^[2]”，液体的密度D_ic与饱和蒸气的密度D_qc相等, 所以式2中的D_ic＝D_qc ，㏑(D_ic/ D_qc)＝，液体表面张力系数α_c,也就随着㏑(D_ic/ D_qc)＝而等于.

式2用精确的数学语言表明：在临界点上，液体的表面张力系数都等于0.与临界点上“表面张力系数等于0^[1]”的实验观测结果完全吻合。

2.4 临界摩尔气体定压热容与定容热容之差的趋同性

应用实际气体的玻尔兹曼因子方程可以推导出摩尔气体定压热容C_Pqm与定容热容C_Vqm之差的理论公式^[5]

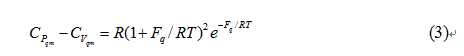
式3表明: 摩尔实际气体定压热容C_Pqm与定容热容C_Vqm之差,不仅只是与压缩功R (普适气体常量)直接相关,而且是玻尔兹曼因子指数- F_q/RT的函数,是一个与分子平均间距(即摩尔体积)直接相关的物理量.

由于C_Pqm与C_Vqm之差的大小变化,百分之百取决于- F_q/RT的大小变化.而各种类型气体的临界玻耳兹曼因子指数- F_qc /RT_c可以近似为经验常量-1.25 ^[5]，所以各种类型气体的临界摩尔定压热容与定容热容之差,也具有趋同的特性.对7种气体实例计算的理论结果^[5], 只有NH₃的相对误差接近2.2 %,其余六种气体全小于0.8 %.充分地证实了趋同性。

3.结论

应用分别描述饱和蒸气与液体两个相的玻尔兹曼因子方程,可以精确描述、准确计算临界点附近物质所呈现的特殊的性质。

参考文献：

[1]  钱尚武，章立源，李椿  热学(第2版)[M]。北京：高等教育出版社，2008. 283、284、272页.

[2]    梁希侠、班士良  统计热力学 第2版[M]（北京：科学出版社）2008. 241、242、248、257页

[3]  于  渌、 郝柏林、陈晓松2005 边缘奇迹 相变和临界现象 第1版 (北京：科学出版社) 第25页. [4]  

[4]  汪志诚 2008 热力学  统计物理(第四版) 北京：高等教育出版社，265—270页

[5]  吴义彬  边缘奇迹:玻尔兹曼因子方法开启了准确计算物质特性的大门 南昌 江西科学技术出版社，2016.9. 

[6]  [美]卡尔L，约斯，陶鹏万，黄建彬，朱大方(译)。MATHESON气体数据手册(第1版)[M]。北京：化学工业出版社，2003