实际气体在“节流过程”中发生温度变化的效应称之为焦耳―汤姆孙效应。节流过程是一个不可逆过程，热力学或统计热力学教材“将达到定常状态的节流过程前后气体的初态和终态近似看作平衡态”^[1]，应用热力学第一定律（能量守恒定律）得出“节流过程为等焓过程^[2]”的结论，进而由此出发导出焦耳―汤姆孙系数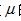的数学关系式^[2]

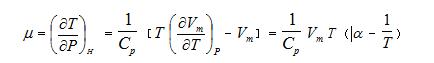
再用上式来解析焦耳 —汤姆孙效应。

显然，上述数学解析用“平衡态”近似地去描述节流过程前后气体的初态和终态，完全回避了节流膨胀制冷的实际物理过程。与上述数学解析不同， 应用实际气体玻尔兹曼因子方程^[3]导出摩尔表面节流焓的理论公式， 就可以紧扣分子之间相互作用力的特性，更清晰、更直观地描述焦耳―汤姆孙效应的实际物理过程。

1、推导摩尔表面节流焓的理论公式

 式(1) 在可实验实测的宏观特性参量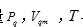与不可实验实测的表面自由能函数F₄之间架起了衔接的桥梁，可以在理论上精确计算摩尔表面自由能F₄。这也就是说，式(1)在定量上实现了精确描述分子间相互作用特性的目标。

摩尔表面熵

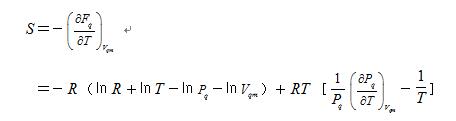
摩尔表面能

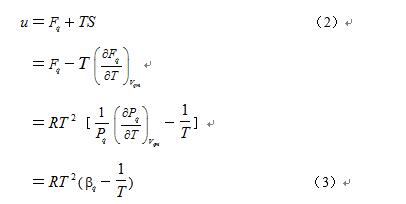
式(2)表明：摩尔表面能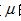等于摩尔表面自由能F₄与摩尔表面分子热运动能TS之和。 这也就是说， 摩尔表面能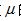不仅仅只是温度T的函数， 而且还与决定分子相互作用特性F₄的分子平均间距(即气体体积)有关。

式(3)中的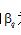为气体定容压强系数。式(3)表明：实际气体的摩尔表面能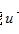可以表示为定容压强系数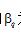与温度T的函数。对于理想气体， 由于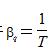，所以理想气体的摩尔表面能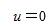， 即理想气体不存在表面区域。

摩尔表面节流焓

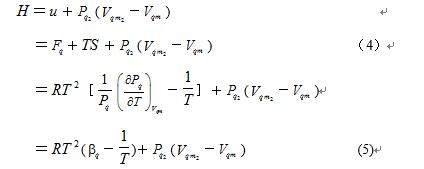
式(4)中的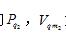为节流后绝热膨胀的压强与摩尔体积。式(4)表明：实际气体体系的摩尔表面节流焓H等于摩尔表面自由能F₄加上摩尔表面分子热运动能TS，再加上摩尔气体在节流之后绝热膨胀过程中必须做的膨胀功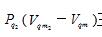三者之和。

2、应用理论公式(4)解析焦耳―汤姆孙效应[注1]

将(4)式改写为

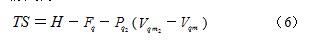
就可以如实地描述节流与膨胀双重制冷效应的实际物理过程。式（6）表明： 在节流、绝热膨胀之后，摩尔表面分子的热运动能TS等于摩尓表面节流焓H减去摩尔表面自由能F₄(数值上等于摩尔气体在节流过程中所必须做的溢出功)、再减去摩尔气体在节流之后绝热膨胀过程中必须做的膨胀功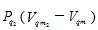。 由于在“节流、绝热膨胀过程”中与外界绝热，摩尔表面节流焓H为定值(能量守恒)， 摩尔表面熵s在“节流、绝热膨胀过程”中只增不减(熵增加原理)，所以摩尔气体分子在节流过程中做逸出功(即节流之后摩尔表面自由能F₄＝0)， 在绝热膨胀过程中做膨胀功(即在“节流、绝热膨胀过程”中，摩尔表面分子的热运动能TS、摩尔表面自由能F₄、膨胀功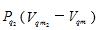三者之间自行转化)，必然导致节流绝热膨胀之后温度T发生变化， 也就是温度T会随着节流之前分子之间相互作用力的特性(摩尔表面自由能F₄的正、负、大小)与所做膨胀功的大小，而产生相对应的变化。如实验测定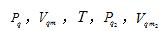，即可由式(1)定量计算出F₄的准确数值，进一步可以由式(6)准确计算节流膨胀之后TS的相应变化。

1.1 对于实际气体体系

（1）当气体分子之间的吸引力大于相邻分子之间的排斥力时，（6）式中的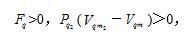，H不变，S不减少，节流膨胀之后摩尔分子热运动能TS小于H，温度T降低。也就是说，在制冷区，气体节流膨胀制冷的物理过程与液体气化膨胀制冷的物理过程（一方面是在气化过程中必须克服表面引力势作用做逸出功，另一方面是逸出液面之后要由液体体积膨胀为蒸汽体积而做膨胀功）完全类同：F₄>0，表示节流过程必须做逸出功，分子热运动能TS减少，降温；在节流之后的绝热膨胀过程中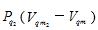，＞0，又必须做膨胀功，分子热运动能TS必然进一步减少，进一步降温。正是由于双重做功的综合效果，才导致节流膨胀的制冷效果比自由膨胀更显著。这也就是“在制冷区，即反转温度以下，焦—汤效应比焦耳效应明显得多，因此节流膨胀较自由膨胀过程降温更为有效^[2]”的原因。

（2）当气体分子之间的吸引力小于相邻分子之间的排斥力时，（6）式中的F₄<0，

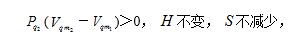摩尔分子热运动能TS的变化有如下3种情况：

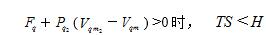，由分子之间的斥力势能作用所增加的分子热运动能，小于绝热膨胀过程中必须消耗的分子热运动能， 所以产生制冷的效果；

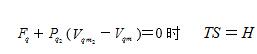，  由分子之间的斥力势能作用所增加的分子热运动能，等于绝热膨胀过程中必须消耗的分子热运动能， 所以温度不变；

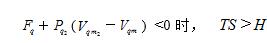， 由分子之间的斥力势能作用所增加的分子热运动能，大于绝热膨胀过程中必须消耗的分子热运动能， 所以制热。

严格意义上讲，正是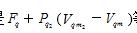等于零时的综合效应导致焦耳―汤姆孙效应存在反转温度的特征。实际的反转曲线是满足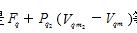＝0时给出的一条曲线。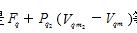的正或负，在“经过”此曲线时改变，故称此曲线为反转曲线，相应的温度为反转温度。所谓反转温度时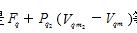＝0，实际气体节流膨胀过程中“温度不发生变化”，是由于气体相邻分子间的斥力势稍稍大于引力势作用，F₄稍小于0时所产生的制热作用，恰好与实际气体绝热膨胀过程中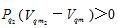所产生的制冷作用相互抵消才出现的一种宏观物理现象。

1.2对于较稀薄的实际气体体系

当且仅当气体分子之间处于完全没有任何作用力的理想状态时，摩尔表面自由能F₄才真正等于零。对于较稀薄的实际气体体系，由于内部分子间相互作用的引力(斥力恒等于零)只是趋近于零，并不等于零，故 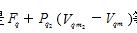中， 第1项F₄也只是趋近于0，并非等于0；第2项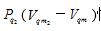恒大于0；两项之和也就大于0。所以，较稀薄的实际气体的节流膨胀过程仍处于靠近反转曲线的制冷区域之内，同样存在双重做功制冷的综合效果，“这就是为什么节流膨胀过程中，即使是较稀薄的气体也容易得到与理想气体性质不同结果的原因^[2]”。

3、结论

相较于“焦耳―汤姆逊系数的数学关系式”， 应用由实际气体玻尔兹曼因子方程导出的摩尔表面节流焓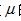的理论公式解析焦耳―汤姆逊效应，就可以实现用简洁的数学语言描述节流膨胀这一不可逆过程的实际物理过程（与液体气化膨胀制冷的物理过程类同）；更加简洁、清晰地解析了为什么“节流膨胀较自由膨胀过程降温更为有效”与“即使是较稀薄的气体也容易得到与理想气体性质不同结果”的客观原因。

参考文献

[1] 汪志诚。热力学、统计物理(第4版)[M]。北京：高等教育出版社，2008。59页。

[2] 梁希侠，班士良。统计热力学(第2版)[M]。北京：科学出版社，2008。91、95、94页。

[3] 吴义彬．实际气体的玻尔兹曼因子方程[J]。江西科学，2011，29(1)：11。

[注1]：

[科学智慧火花]2012-07-20<<焦耳―汤姆孙效应的数学解析>>文稿中，使用公式

本文在予以纠正的同时，对这种十分不应该出现的基本物理概念错误，表示深深的歉意！