1.“曳物线”与“伪球面”

从曲线C上某一动点P的切线与某一定直线l的交点Q到点P的线段长恒为定值，则称曲线C为曳物线。直线l为其渐近线。^［1］

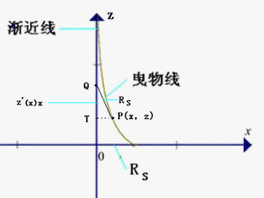
图1 “曳物线”

由“曳物线”绕其渐近线旋转而形成的回转曲面叫做“伪球面”。这种曲面的全曲率在每一点都是常数且是负的。^［1］

考虑OXZ平面上的曳物线：如果曲线C上任意一点P的切线与z轴的交点Q到点P的线段长恒为定值R_S，则称曲线C为曳物线。z轴称为曳物线的渐近线。

设曳物线C的方程为z=z(x)。若曳物线C上一点P(x，z)处的切线方程为Z-z=Z^’(x)(X-x)，则切线与z轴的交点为Q(0，z-Z^’(x)x)。

由∣PQ∣=R_S，可知：在直角三角形△PTQ中，∣PQ∣²=∣QT∣²+∣TP∣²，即R_S²=（Z^’(x)x）²+x²，可得Z^’(x)=±(√R_S²-x²)/x，亦即dz=±（(√R_S²-x²)/x）dx。

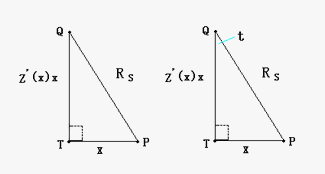
图2

令x=R_Ssint（0＜t≤π/2），有dz=±R_S（cos²t/sint）dt=±R_S（(1-sin²t）/sint）dt=±R_S(1/sint-sint）dt=±R_S(1/(2tan(t/2)cos²(t/2))-sint）dt，即：dz=±R_S(1/(2tan(t/2)cos²(t/2))-sint）dt，于是有：z=±R_S(lntan(t/2)+cost）。

于是，OXZ平面上以z轴为渐近线、定值为R_S的曳物线方程是①：

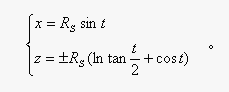
上述以z轴为渐近线、定值为R_S的曳物线，绕它的渐近线z轴旋转而形成的回转曲面——“伪球面”R_S，其在OXYZ直角坐标系中的参数方程是②：

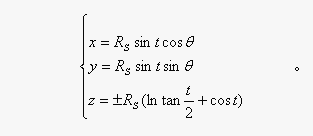
其中，0≤θ≤2π。

称“伪球面”内的“渐近线”为“伪球面的球心” ^［2］。下图所示的“喇叭形”，就是一个以R_S为半径的“伪球面”。^{［3］［4］}

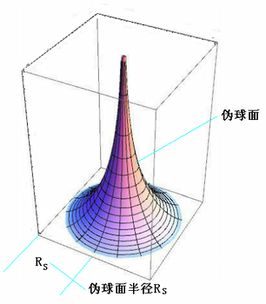
图3 “伪球面”

在这里，“伪球面”的“球心”是一条直线——“伪球面”内的“渐近线”——形成“伪球面”的“曳物线”的“渐近线”。

我们的讨论认为，“奇点视界”就是一个“伪球面”，还是一个“三维球面”：在“四维空间”中，其中的“任意一点” ——都是由一个“点”——“奇点”“大爆炸”而来——与“奇点”等距。^{［5］［6］}

2.“伪球面”的曲率

对于上述的“伪球面”R_S的曲率K，可以用下述的“回转面曲率公式” ③计算^［7］：

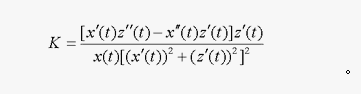
把x(t)=R_Ssint，x^’(t)=R_Scost，x^’’(t)=-R_Ssint，z^’(t)=R_Scos²t/sint，z^’’(t)=-R_S(cost+sin²tcost)/sin²t代入③，计算可得：K=-1/R_S²。即④:

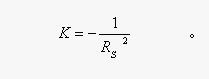
或者通过曲线“参数曲率公式” ⑤计算^［7］：

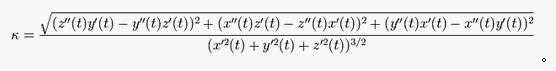
把x(t)=R_Ssintcosθ，x^’(t)=R_Scostcosθ，x^’’(t)=-R_Ssintcosθ，y^’(t)=sinθcost，y^’’(t)=-sinθsint，z^’(t)=R_Scos²t/sint，z^’’(t)=-R_S(cost+sin²tcost)/sin²t代入⑤，计算可得到曲线向与法向同向的一个主曲率k₁=1/R_Scott。^［8］

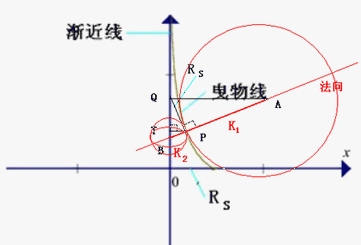
图4

另外，如下图，在P点，与“伪球面”母线向与法向同向的“密切圆”⊙A的半径为r₁，在直角三角形△APQ中，r₁/R_S=cott,可知k₁=1/r₁=1/R_Scott；在P点，与“密切圆”⊙A“正交”的且“反向”的“密切圆”⊙B的半径为r₂，而在直角三角形△BPQ中，r₂/R_S=tant,可知k₂=-1/r₂=-1/R_Stant，因此，还可以得到另一个反向的主曲率k₂=-1//R_Stant，所以K=k₁k₂=-1/R_S²，即K=-1/R_S²。

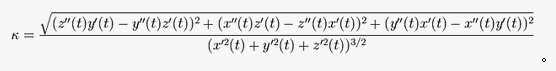
图5

可见，对于半径为R_S的“伪球面”上的任意一点P，其高斯曲率为K=-1/R_S²，两个主曲率分别为k₁=1/R_Scott和k₂=-1/R_Stant。“伪球面”具有“双曲面”特征：“伪球面”向两个“正交”的、相反的方向“弯曲”——高斯曲率中的一个主曲率为正、一个主曲率为负。^［8］

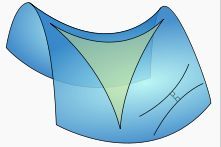
图6

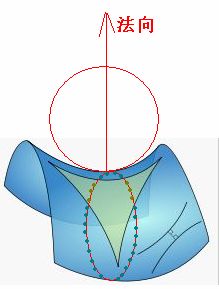
图7

3.“质量”与“能量”

在“宇宙空间”中，存在“伪球面”吗？怎样的“空间条件”下？或者说是怎样的自然作用下？可以产生这种“伪球面”上“正交”的正、负曲率：k₁=1/R_Scott和k₂=-1/R_Stant——“同时向两个相反方向弯曲的曲面或空间效应”？

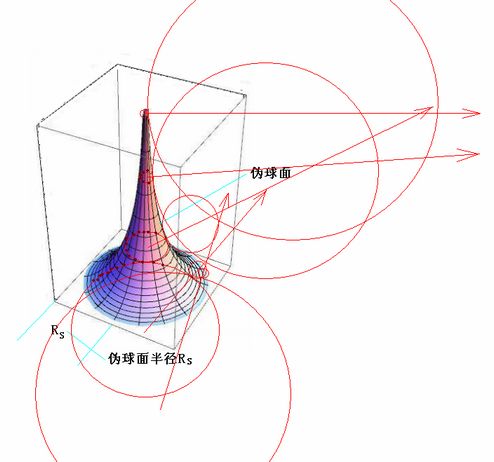
图8

“质量”与“能量”：“质量”的“点”聚集、“万有引力”，“能量”的从“点”出发、向外膨胀；“引力”与“反引力”：“引力”的“相互吸引”、向中心聚集，“反引力”的“相互远离”、空间膨胀——方向相反——他们在空间中的作用效果会产生“同时向两个相反方向弯曲的曲面或空间效应”吗？

我们的“宇宙空间”是由一个“引力场”（“质量”）和一个“反引力场”（“能量”）共同组成的。^［2］其中的“反引力场”的“中心”就可以形成一个“伪球面”空间——下图中的“蓝色空间”。^［2］

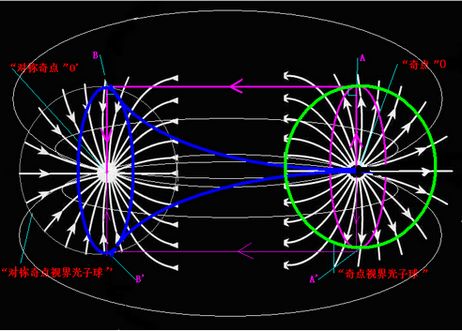
图9

4.“曲率”与“压强”

爱因斯坦的宇宙学常数或真空能预言状态方程w（压强与能量密度之比值）不随时间而变、且恒为W=-1。^{［9］［10］}

若设一个空间内的“能量密度”为ρ₀，压强为p，则由w=-1，即w=p/ρ₀=-1，亦即p/ρ₀=-1，可得“负压方程”：p=-ρ₀。

如果在半径为r的球(体积V=（4/3）πr³，π为圆周率)内，拥有的能量为E，那么p=-ρ₀=-E/V=-（3/4π）E/r³。即有“负压方程”：

p=-（3/4π）E/r³

可见，半径为r的球面上的“负压”p，与球内的能量E成正比，与到能量中心（球心）的距离的三次方成反比。因此，在一个“光子负压球体”中，从球面到球心，“负压”越来越大（指绝对值）。

图10

若设质量为M的“奇点”O的“视界”半径为R_S，则根据史瓦西半径公式有R_S=2GM/C²（G为引力常数，C为光速），由质能方程有E=MC²，于是M=C²R_S/2G，M=E/C²。

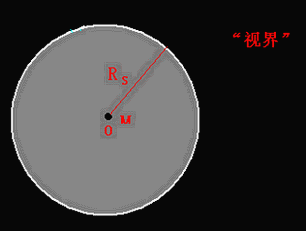
图11

假定在“质能方程”下，“奇点”质量蕴含的能量在其“视界”上产生的“压强”p符合上述的“负压方程”，则可以有：

p=-（3/4π）E/R_S³=-（3/4π）MC²/R_S³=-（3C²/4π）M/R_S³

=-（3C²/4π）（C²R_S/2G）/R_S³=-（3C⁴/8πG）/R_S²

=（3C⁴/8πG）（-1/R_S²）。

如果上述“视界”在半径为R_S的“伪球面”上，那么该“视界”曲面的曲率K=-1/R_S²，所以有：p=（3C⁴/8πG）（-1/R_S²）=（3C⁴/8πG）K，即p=（3C⁴/8πG）K，亦即K=（8πG/3C⁴）p，于是有⑥：

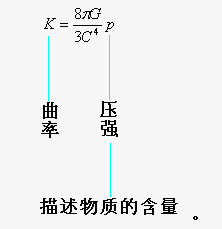
又因为K=-1/R_S²=k₁k₂=（1/R_Scott）（-1/R_Stant），所以K=（1/R_Scott）（-1/R_Stant）=（8πG/3C⁴）p，即有⑦：

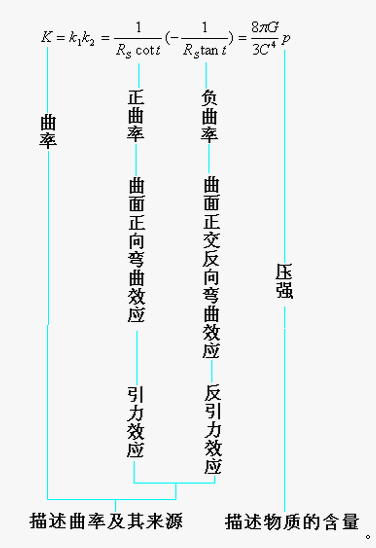
5.“曲率”与“物质”

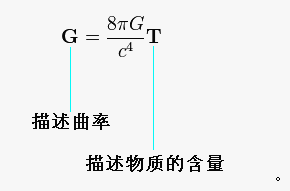
在广义相对论中，度量张量和黎曼曲率张量是定义在时空中的每一点的量。时空中的物质定义了：能量-动量张量“T”，时空中的弯曲定义了：爱因斯坦张量“G”。“时空告诉物质如何运动，物质告诉时空如何弯曲”的原理意味着这些量必须互相联系。于是，爱因斯坦场方程可以表示成⑧（“G”（描述曲率）可以换算成“T”（描述物质的含量））：^［11］

参考资料:

［1］《曳物线》百度百科

［2］《“伪球面”——“宇宙的另一极”》

［3］《伪球面》百度百科

［4］《伪球面、常高斯曲率曲面》百度文库

［5］《我们在“奇点视界”—“三维球面”之中》

［6］《“三维球面”是一个“‘伪球面’空间”》

［7］《曲率》维基百科

［8］《高斯曲率》维基百科

［9］《状态方程 (宇宙学)》维基百科

［10］《高能所等在暗能量研究方面取得新成果》中科院高能物理研究所

［11］《广义相对论入门》维基百科

［12］相关资料请参考《“引力场”与“空间场”》

（杨明昆 王严学 杨昭国 期待您的交流、讨论ygyzg@126.com)