“热力学的统计理论（即微观的）基础的发展是十九世纪物理学的卓绝成就之一。虽然， 这个发展的许多观念都源出于麦克斯韦和玻耳兹曼，但正是吉布斯的工作更直接地影响着我们现代对平衡态统计力学的表述^[1]”； “在统计物理学中，物态方程可以根据系统内微观粒 子的属性采用统计物理原理(吉布斯的系综方法)获得。然而，从单个粒子属性到理论上計算 出系统的宏观量并不是一个很简单的问题，需要根据粒子的特性建立统计模型，求出系统 平衡时处在各微观态的概率分布函数，然后由分布函数計算出大量微观粒子系统的各微观量的统计平均，即宏观量。在利用分布函数求统计平均时往往还需要利用各种近似算法。^[2]” 要在定量上得到精确的计算结果，更加“不是一个很简单的问题” ！

与“系综方法”不同，直接从玻耳兹曼分布出发，在平衡体系边界区域的表面保守力 场中应用玻尔兹曼分布，导出分别描述气体与液体的玻尔兹曼因子方程，不仅可以对液体的相变潜热^[3]、表面张力系数及其温度变化率^[4]等在定量上进行准确的数值计算，而且也 可以对自然界物质在“临界点、沸点、熔点”时的物理特性进行准确的数学描述。

1.临界点特性——气体临界系数存在趋同的特性

文献[5]3.1节对“气体数据手册^[6]”中所列156种气体进行数值计算分析表明：在20%误差范围之内，94.23%的各种类型气体的临界系数都可近似为3.490，即

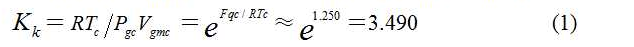
(2)表明：应用临界玻尔兹曼因子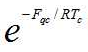倒数的趋同性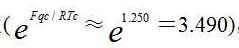，描述气体临界系数K_K 的趋同特性，明显比范世普适常量（2.667）更加切合实际，物理意义也更加明晰。

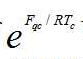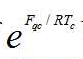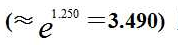简明的数学语言可以描述各种气体临界系数K_k  的精确数值；的趋同性则可以描述绝大多数气体临界系数的趋同性。

2.临界点特性——液体表面张力系数都等于零

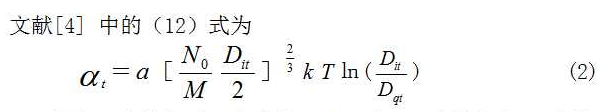
(2)式表明，液体表面张力系数α_t是温度T、液体密度D_it与饱和蒸汽的密度D_qt的函数。

 由于临界点上“液体及其饱和蒸汽间的一切差别都消失了^[7]”，液体的密度与饱和蒸汽的密度相等，所以(2)式中的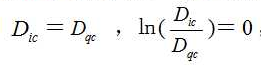，液体表面张力系数α_c，也就是随着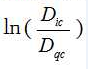等于0而等于0。

(2)式用简洁的数学语言表明：临界点上液体的表面张力系数都等于零，与临界点上“表面张力系数都等于[7]”的实验观测结果完全吻合。

3.沸点特性——沸点摩尔气化熵大同小异，通常为10R

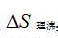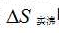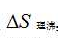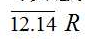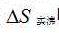文献[3]表2中的数据表明，定量计算五种液体沸点摩尔气化熵的理论数值，不仅与实验观测值直接计算的实验观测吻合得非常好，而且五种液体的的平均值为，的平均值为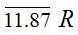，两者的相对误差仅为2.27% ，都与“沸点摩尔气化熵大同小异，通常约为10R。”基本一致。这也是既从纯理论计算角度，也从实验观测值计算角度，论证了沸点特性——禇鲁统规则。

禇鲁统规则不仅仅只是由实验观测值定量计算得到的实验规则，同时也是可以是由纯理论公式定量计算论证的物理定律(又称特罗顿定律)。

4.熔点特性——冰升热与熔解热的数值计算

(1)冰升华热的数值计算

2014年6月9号在《科学智慧火花》上发布的《在定量上精确计算冰的升华热》，给出了升华热的理论计算值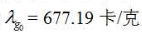：；且理论计算值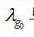与实验观测值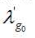(677.12卡 /克^[8])相比较，相对误差很小：。

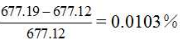(2)冰熔解的数值计算

由文献[3]表1查得：0℃时水气化热的理论计算值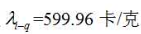，可以用0℃时冰升华热的理论计算值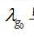与0℃是水气化热的理论计算值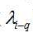^[8]的差作为0℃时冰熔解的理论计算值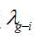，即：

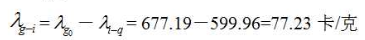
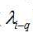相对于熔解热的实验观测值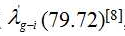，相对误差为。

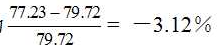数值计算表明：冰升华热与熔解热的理论计算值与实验观测值都吻合得很好。

结论：应用气体、液体与冰的玻尔兹曼因子方程，对自然界物质在”临界点、沸点、熔点“时的物理特性进行数学描述的结果，与实验观测值吻合得很好。事实表明：简单的数学语言可以在很宽的温度范围内准确描述自然界物质物态变化的客观规律；玻尔兹曼因子方程是更具普适性的物态方程。

 参考文献：

[1] 杨振宁 戴定国 译  相变与临界现象的引论性评注  低温与超导   1985年第1期. 76页。

[2] 汤文辉 张若棋  物态方程理论及计算概论 第2版 (北京 高等教育出版社) 2008.13页。

[3] 吴义彬 汽化热与沸点汽化熵的理论计算 物理通报 2013年第7期 90页。

[4] 吴义彬 饱和蒸汽压下单元液体的物态方程及其应用[J]. 江西科学，2010,28(5):593。

[5] 吴义彬 实际气体的玻尔兹曼因子方程[J].江西科学，2011,29(1):11。

[6] [美]卡尔L.约斯，陶鹏万，黄健彬，朱大方(译) MATHESON 气体数据手册(第1版)[M], 北京：化学工业出版社，2003。

[7] 钱尚武 章立源 李椿 热学(第2版)[M]，北京：高等教育出版社，2008,272页。

[8] 王竹溪 2005，热力学，第2版(北京：北京大学出版社) 161页。