1.“空间弯曲”

物质实体运动所发生的部分，称为“空间”。 ^［1］

爱因斯坦的广义相对论认为，由于有物质的存在，空间和时间会发生弯曲，而引力场实际上是一个弯曲的时空。 ^［2］

在广义相对论中，引力被描述为时空的一种几何属性（曲率）。 ^［3］

图1 “引力”与“空间弯曲”示意图

图2“空间弯曲”示意图

图3 “引力”是一种“空间弯曲”

如果把静止“质量”为m₀、曲率半径为r₀的“质点”，在速度为v的情况下的“质量”设为m、曲率半径为r，c为光速，那么根据相对论的“尺缩效应”，在速度v的方向上有r=r₀√1-(v/c)²。

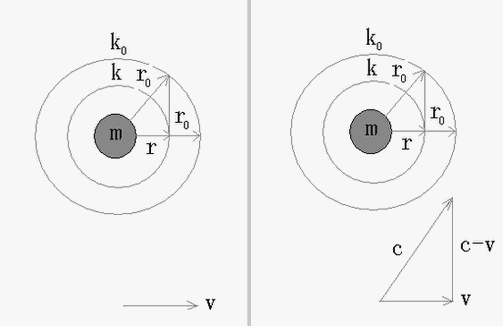
图4 “空间弯曲”与“速度”

若设“质量” m对应“空间”的曲率为K， 由k=1/r，k₀=1/r₀，r=r₀√1-(v/c)²，则有k=k₀/√1-(v/c)²。

k=k₀/√1-(v/c)²说明，静止“质量”m₀以速度v运动后，其对应的“空间曲率”会发生“增大”变化——“速度弯曲空间”。 ^［4］

2.“空间平直”

既然“引力场”是“弯曲”的“空间”——“引力场”即“弯曲空间”，那么，“反引力”，就应该考虑与“弯曲空间”相反的情形：“平直空间”。

若设质量为m的质点，绕质量为M的中心质量做圆周运动，环绕速度大小为v，则有：速度v对质量为m的质点所对应的“空间”施加了“弯曲”作用——“速度弯曲空间”。“弯曲”的能力量度，是“相对论因子”√1-(v/c)²。

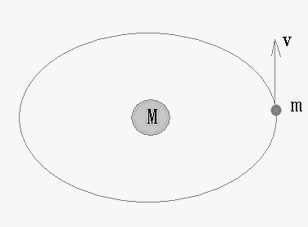
图5 “速度弯曲空间”

在这里，我们假定（先假定、再验证）：速度v对质量为m的质点所对应的“空间”施加了“弯曲”作用的同时，对中心质量M所对应的“空间” 也施加了“平直”作用——“速度平直空间”。“平直”的作用方式，符合“右手定则”——“轴向平直”， “平直”的能力量度，也是“相对论因子”√1-(v/c)²。

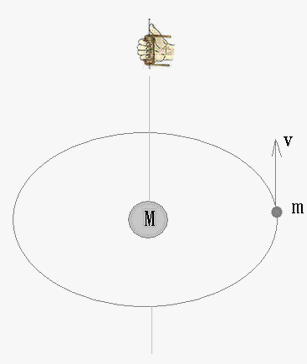
图6 “轴向平直”

即如果中心质量M原来所对应的“空间曲率”为K₀，那么在速度v的作用下，发生“平直”，其对应的“空间曲率”“减小”为：K=K₀√1-(v/c)²。致使“中心质量”“减小”为：M√1-(v/c)²——“反引力”效应。

通俗地，可以说地球的公转速度，使得太阳的“质量减小”。

但是，一般的，如同“速度弯曲空间”一样，“速度平直空间”的宏观表现都很微弱，不易觉察，难以检测。

3.“实验检测”

3.1“持久强电流”

超导材料，又称为超导体，指可以在在特定温度以下，呈现电阻为零的导体。零电阻和抗磁性是超导体的两个重要特性。使超导体电阻为零的温度，叫超导临界温度。

为了证实（超导体）电阻为零，科学家将一个铅制的圆环，放入温度低于Tc=7.2K（0K=-273.15℃；K开尔文温标，起点为绝对零度）的空间，利用电磁感应使环内激发起感应电流。结果发现，环内电流能持续下去，从1954年3月16日始，到1956年9月5日止，在两年半的时间内的电流一直没有衰减，这说明圆环内的电能没有损失，当温度升到高于Tc时，圆环由超导状态变正常态，材料的电阻骤然增大，感应电流立刻消失，这就是著名的昂内斯持久电流实验。 ^［5］

1991年10月，日本原子能研究所和东芝公司共同研制成核聚变堆用的新型超导线圈。该线圈电流密度达到每平方毫米40安培，为过去的3倍多，达到世界最高水准。该研究所把这个线圈大型化后提供给国际热核聚变堆使用。这个新型磁体使用的超导材料是铌和锡的化合物。 ^［6］

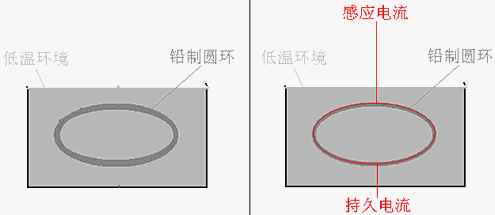
图7 “持久强电流”

3.2“旋转质点”

在一定条件下，“圆环形”“超导体”可以获得“持久”的“强电流”：“超导圆环强电流”。而电流是“定向运动的电荷”，每一个电荷都有质量。如果只考虑质量，这些“电荷”都可以看成一个“质点”——“电荷质点”，所以，“超导圆环强电流”也可以说是“超导圆环旋转的质点”——“圆周运动的质点”。

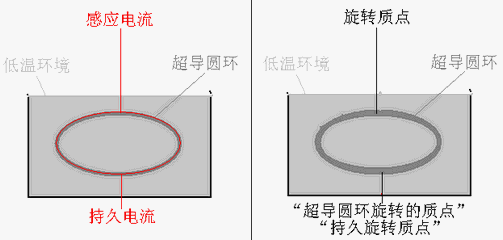
图8 “旋转质点”

3.3“超导圆盘”

如果在一个“中空绝缘圆盘”（低温下也是绝缘的）上，嵌入固定布列很多“同心”的、相互绝缘“超导圆环”O₁、O₂、O₃……在满足“超导”所必需的“低温”等条件的前提下，再利用电磁感应，使得所有“超导圆环”内，激发起感应电流——“强电流”，那么在这个圆盘上，这些“超导圆环强电流”，都产生了许许多多的“超导圆环旋转的质点”：“旋转圆环圆盘”——尽管圆盘“看起来”并没有旋转——“虚拟的旋转圆环圆盘”，称为“超导圆环圆盘”或“超导圆盘”。“超导圆盘”是“轴对称”的，“旋转轴”就是“对称轴”。

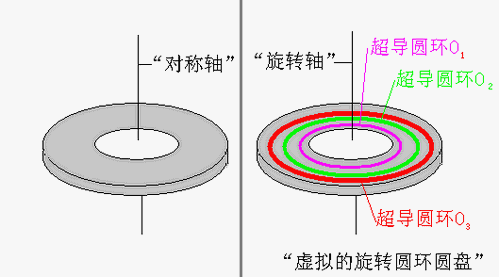
图9 “超导圆盘”

3.4“超导圆筒”

把若干个上述“虚拟的、中空的旋转圆环圆盘”，上下叠加成为一个“圆筒”，他们的“旋转轴”都是重合的，并保证其中的任意两个“超导圆环”相互之间都是绝缘的，称为“虚拟的旋转圆环圆筒”或“超导圆环圆筒”或“超导圆筒”。

图10 “超导圆筒”

如果利用电磁感应使得“超导圆筒”上所有“超导圆环”内，都激发起感应电流——“强电流”，那么同样地，在这个圆筒上的“超导圆环强电流”，就会形成“巨量”的“虚拟的旋转圆环圆筒质点”。

3.5“重心失重”

根据右手定则，这些作“圆周运动”的“电荷质点”的“速度”，使得圆筒对称轴的“空间”趋向“平直”——引力减小——“反引力”效应。而这种“平直”作用的能力量度也应该是“相对论因子”√1-(v²/c²)（v为绕圆筒对称轴旋转的“电荷”“质点”的速度、c为光速）。所有“超导圆环”内形成“感应电流”的“电荷”“质点”，都在绕圆筒对称轴高速旋转，都共同对“圆筒对称轴”的“空间场”发生“平直”“作用”——“轴向平直”，使得“重心”在“圆筒对称轴”的物体的重力减小。 并且，这些“巨量”“质点”的“速度平直空间”的作用叠加效应，就会表现得比较明显，产生宏观效果：可以用仪器检测出“轴向平直”的作用——“重量变轻”——“反重力”！

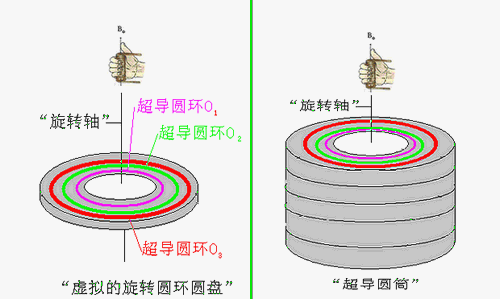
图11 “超导圆筒”

这时，把一个用绝缘的、不能被磁化材料做成的圆柱体（排除磁化对实验的影响），悬挂在一个弹簧秤下，放入“超导圆筒”中，让圆柱体的“重心”与“超导圆筒”的“对称轴”“重合”，比较放入前后弹簧秤的读数。并且，“超导圆筒”要处于“低温超导环境”里，进入“超导”“强电流”工作状态，同时，为排除磁场对读数的影响，要把弹簧秤置于“磁屏蔽环境”里。

如果放入后的读数小于放入前的读数——“重量变轻”，那么就可以证明“超导圆筒”能够产生“反重力”效应。

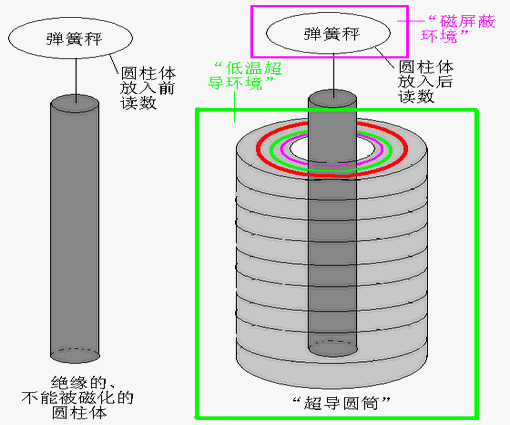
图12 “重心失重”

恳请广大读者朋友，利用“超导圆筒”的“强电流”进行实验，来检测“反重力”——验证“反引力”。

参考资料:

［1］《空间》百度百科

［2］《阿尔伯特·爱因斯坦》百度百科

［3］《引力》维基百科

［4］《“速度弯曲空间”》

［5］《超导体》百度百科

［6］《超导》百度百科

［7］相关资料请参考《“引力场”与“空间场”》

杨明昆 王严学 杨昭国期待您的交流、讨论：ygyzg@126.com。