摘要：本文提出的“孪生素数求解公式”是在"求任意两数之间素数的公式"的基础上推导得出的。该公式能够精确地求出任意区间内的所有孪生素数对。这一成果填补了初等数论领域长期以来缺乏有效孪生素数求解方法的空白。该公式的建立为研究孪生素数猜想等数论难题提供了新的研究工具和理论支持。文章的最后，补充介绍了“孪生素数构造式”的分析和证明。

关键词：任意两数之间；孪生素数；公式；边界处理；等价区间；孪生素数构造式。

Abstract:The "Twin Prime Calculation Formula" proposed in this paper is derived based on the "Formula for Finding Primes Between Any Two Numbers.” This formula can accurately determine all twin prime pairs within any given interval. This achievement fills a long-standing gap in elementary number theory, where effective methods for calculating twin primes were lacking. The establishment of this formula provides newl research tools and theoretical support for studying number theory challenges such as the Twin Prime Conjecture. Finally, the paper supplements the analysis and proof of the "Twin Prime Construction Formula."

Keywords: between any two numbers; twin primes; formula; boundary handling; equivalent interval; twin prime construction formula.

1.解决孪生素数猜想有哪些困难？

解决“孪生素数猜想”（即“是否存在无限多个孪生素数对”）

的困难主要来自以下几个方面：（总结的不一定很全面，但总体大概就是这几个方面。)

（1）素数分布的不规则性

—素数在自然数中的分布看似随机，没有简单的显式公式可以精确预测下一个素数的位置。

-虽然素数定理(Prime Number Theorem)给出了素数分布的渐 进行为（即\(\pi(n)\sim \frac{n}{\In n}\)),但它无法直接 用于研究孪生素数的具体分布。

（2）孪生素数的稀疏性

—随着数字增大，孪生素数对的密度逐渐降低（如\（（3，5），（5，7），（11，13）\）在100以内较多，但1000以内就少得多）。

—目前已知的“孪生素数计数函数”（即\（\pi_2（n）\），表示不超过\（n\）的孪生素数对的数量）的估计是：

\[\pi_2(n) \sim C \frac{n} {(\In n)^2}, \quad \text {其中 } C \approx 1.32032 \text{(孪生素数常数)}\]

但这一估计尚未被严格证明。

（3）缺乏有效的解析工具

—许多数论问题（如哥德巴赫猜想、黎曼猜想）可以通过复分析（如zeta函数）来研究，但孪生素数猜想尚未找到类似的强大工具。

筛法（如陈景润的加权筛法）可以证明“存在无限多个素数N（pV），使得\（p+2\）是素数或半素数”，但无法直接推广到纯孪生素数。

（4）现有方法的局限性

张益唐的突破（2013）：证明了“存在无限多个素数对\（（p，p+h）\),其中\(h \leq 7000\)”（后来改进到\(h\leq 246\）)。

这表明孪生素数猜想在“有界间隔”上取得了进展，但距离\（h=2\）（即真正的孪生素数）仍有很大差距。

多项式方法：类似“格林-陶定理”(Green-Tao Theorem)证明 “素数中存在任意长的等差数列”，但尚未能推广到孪生素数。

（5）计算验证的局限性

虽然计算机已经找到大量孪生素数对（如目前已知最大的孪生素数对是\(2996863034895\times2^{1290000}\pm1\)),但计 算无法证明“无限多”的存在性。

(6)总结

孪生素数猜想的困难主要在于：

①素数本身的分布难以精确刻画；

②现有的解析工具（如筛法、复分析）尚未能完全适用于该问题；

③张益唐等人的工作缩小了间隔，但尚未达到\（h=2\）；

④计算验证无法替代数学证明。

目前，该问题仍然是数论中最著名的未解决问题之一，其解决可能需要全新的数学工具或理论突破。

（7）本文的研究思路与方法的创新性

在探索孪生素数等数论难题时，我想，完全照抄别人的内容是肯定不可行的，尤其是对于普通的数学爱好者而言，单纯追随数学家的既有路径往往难以取得实质性进展，必须自我寻找解决问题的方法。通过多年的探索，我觉得，突破传统思维框架至关重要。唯有采用全新的视角和方法，才有可能实现理论突破。

基于这一理念，我将自己的研究策略分为两个阶段：

①建立精确的孪生素数求解公式：首先构建一个能够准确计算任意区间内孪生素数对的数学表达式；

这是本章所要解决的问题。

②多尺度分析方法：在公式的基础上，结合宏观（整体分布规律）、微观（局部素数结构）以及宏微观相互作用的研究方法，系统性地推进孪生素数猜想的解决。

后面，再用两章来解决这方面的问题。

这一研究路径旨在通过理论创新与多维度分析，为破解这一经典数论难题提供新的可能性。

2.求任意两数之间孪生素数的公式

（1）前面，我们推导出了“求任意两数之间素数的公式”。基于此公式，我们进一步拓展得到了“求任意两数之间孪生素数的公式”。

公式2：任意两自然数间孪生素数求解公式

对于任意自然数n到N之间的孪生素数对数，可用以下公式计算：

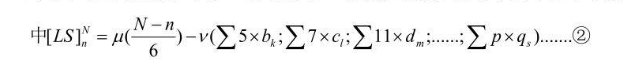
 说明：

（1）公式中的[符号1]表示n到N之间所有孪生素数的对数（注意：此处使用中文自定义符号，必须同时考虑需要求出数值和数对）

（2）[符号2]表示n到N之间所有候选数对的个数（分母为6）。需注意的是：为确保计算结果始终为整数且准确，需对n和N进行预处理（此即表示如何找出候选数对）：数型预处理规则：

①若n或N为能被3整除的奇数，保持原值不变；

② 若n或N为被3除余1的奇数，则加2使其能被3整除:

③ 若n或N为被3除余2的奇数，则减2使其能被3整除;(简记口诀:“余1加2，余2减2”)

④若n或N为偶数:(继续判定如何找出候选数对)

a) 能被3整除的偶数:n加3，N减3，转化为能被3整除的奇数3；

b) 其他形式的偶数:先减1(n)或加1(N)转化为奇数，再按奇数规则处理。

示例:μ[(39-15)/6]=4，即在15与39 之间有4组候选数对:17-19、23-25、29-31、35-37

[符号 3]表示所有需要排除的奇合数对。与素数公式不同之处在干:(作为减数，减去这一部分内容，即可求得所需的结果)

a)此处不需要考虑因子3的影响(因为被减数中的数值已经全部除以 6，剩下所取的都是一组组不能被3整除的奇数);

b)每次必须同时排除两个连续的奇数(无论另一个是否为素数);

c)排除操作以数对为单位进行。

应用示例:在15-39 范围内，排除5x5=25 和5x7=35 时，需同时排除其相邻奇数 23和37.最终剩余两组孪生素数:17-19和29-31

（2）定理证明（对公式②的证明）

设区间[n，N]内所有满足t≠0mod3的奇数为研究对象：

③孪生素数筛选性

对剩余素数集进行配对筛选：

建立相邻素数对集合{（p，p+2）|p，p+2∈剩余素数集}排除所有孤立素数（即不满足p+2或p—2同为素数的素数）最终所得即为严格意义上的孪生素数对。

（3）除了以上的证明以外，还有一个较为简单的证明：

证明：在公式②中，设t为n到N间不能被3整除的奇数，（1）若t为合数，必然为以下因式分解中的一个：

t=5xb,7xc,11xd......, pxq.(n<=t<=N)

所以，任何一个奇合数t都不可能留在下式之中：

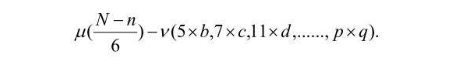
当被减数中的这些“不能被3整除的奇数数组”减去所有的奇合数之后，留下的数字必然都是素数；

（2）在留下的这些素数中，对于所有单个的、不能成双成对的素数再全部划去，这样，剩下的素数必然都是一对一对的孪生素数。

证毕。

3.孪生素数公式应用实例

（1）实例1：求区间（43， 71）内的孪生素数

①边界处理

②等价区间：计算（45， 69）的孪生素数与原问题等价。

③公式计算

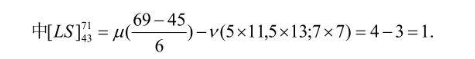
即：在43与71之间有1对孪生素数，它们是： 59     61

（2）实例2：求区间（147， 253）内的孪生素数

①边界处理

②等价区间：（147， 255）。

③公式计算：

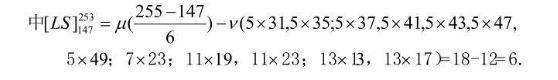
这 6 对孪生素数是：149 151   179 181  191 193 197 199   227 229   239 241

（3）实例3：求偶数区间[1058，1174]内的孪生素数①偶数转换

1058→1058—1=1057（奇化）

1174→1174+1=1175（奇化）

②边界处理

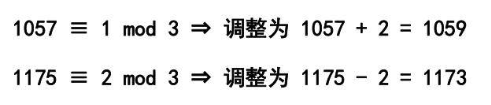
等价区间：（1059，1173）。

③公式计算

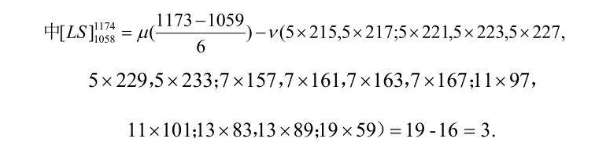
即：在1058与1174之间有3对孪生素数，它们是：1061 1063 1091  1093 1151   1153.

（4）实例4：求偶数区间[18，102]内的孪生素数

①边界处理

②等价区间：（21，99）。

③公式计算

(5)公式说明

①通用步骤

A.奇偶处理：偶数区间需转换为奇数区间。

B.模3修正：根据边界数模3余数调整（余1加2，余2减2，余0不变)。

C.核心公式：

[\text{孪生素数对数} = \left \ Ifloor  \frac{T - n}{6} \right\rfloor  -  \text{合数修正项}]

D.双重含义

利用本公式，既可计算孪生素数对数，亦可定位具体数值。

4.孪生素数构造式的分析与证明

（1）公式定义：给定一个自然数n，定义“孪生素数构造式”（TwinPrime Construction Formula)为：

（此即为求孪生素数公式的第二种表现形式）

TwinP(n) = {p∈P(n) | p+2∈P(n+2)}.

其中：P（n）表示不超过n的所有素数的集合。TwinP（n）表示不超过n的所有“孪生素数对中的较小素数” （即p和p+2均为素数）。

（2）公式说明：孪生素数：（TwinPrimes）是指相差2的一对素数，如（3，5），（5，7），（11，13）等。

该构造式的作用是：给定一个上限 n，筛选出所有满足p≤n且p+2也是素数的素数p。

由于p+2可能超过 n，因此P（n+2）确保p+2也在素数范围内被检查。

（3）构造式的正确性分析：要证明该构造式正确，需验证：

①所有TwinP（n）中的p确实构成孪生素数对；

由定义，p∈P（n），即p是素数且p≤n。p+2∈P（n+2），即p+2也是素数且p+2≤n+2。因此，（p，p+2）是一对孪生素数。

①所有不超过n的孪生素数对中的较小素数都被包含在TwinP（n）中：设（q，q+2）是任意一对孪生素数，且q≤n。

②由于q≤n，且q是素数，故q∈P（n）。由于q+2是素数且q+2≤n+2,故q+2∈P(n+2)。因此，q∈TwinP(n)。

综上，该构造式“完全覆盖且仅覆盖”所有不超过n的孪生素数对中的较小素数。

（4）构造式的计算方式：

①在实际计算中，TwinP（n）可以通过以下步骤生成：生成P（n+2），即所有不超过n+2的素数。遍历P（n），检查每个素数p是否满足p+2∈P（n+2）。收集所有满足条件的 p，构成 TwinP（n）。

②示例验证： 例1：计算TwinP(10)

结果：TwinP（20）={3，5，11，17}，对应孪生素数对（3，5）、（5，7）、(11,13)、(17,19)。

从以上的举例来看，这第二种“求孪生素数的构造式”看起来比较简单，但求孪生素数的过程比较烦杂，不如第一种方法简单适用，特别是遇到数字较大时，因此，在今后的实际计算中，我们大多采用第一种方法。

(5)数学意义：

A.该构造式“形式化”了孪生素数的定义，并提供了明确的筛选方法：

B.可用于研究孪生素数的分布规律，例如：计算|TwinP（n）（不超过n的孪生素数对数）。

验证孪生素数猜想（是否存在无限多对孪生素数）。

(6)可能的扩展：

A.广义孪生素数：若定义 TwinP(n,k)={p∈P(n)|p+2k∈ P（n+2k）}，可研究间隔为2k 的素数对（如（p，p+6）称为“性感素数”)。

B.高效算法：结合筛法（如埃拉托斯特尼筛法）优化计算TwinP(n).

(7)总结：

A.构造式：TwinP(n)={p∈P(n)|p+2∈P(n+2)}严格定义了孪生素数的生成规则。

B.正确性：通过集合论和素数性质证明了其完备性。

C.应用：可用于理论研究和实际计算，它和“求孪生素数的公式”一样，同样是研究孪生素数问题的有力工具。

5.全文总结：

本文围绕孪生素数的求解公式及相关构造式展开研究，主要探讨了以下三方面的内容：

（1）提出了解决孪生素数猜想的困难

孪生素数猜想是数论中的经典难题，其核心在于证明“存在无穷多对相差2的素数（即孪生素数）”。尽管近年来张益唐等数学家在该领域取得突破性进展（如证明存在无穷多对素数间隔小于某个有限值），但彻底解决该猜想仍面临巨大挑战。困难主要源于素数分布的不可预测性，以及现有筛法、解析数论工具在精确刻画素数对时的局限性。

（2）找到了求任意两数间孪生素数的公式（包括两种形式）其重大意义在于：

A.突破数论难题：为孪生素数猜想（是否存在无穷多对孪生素数）提供直接验证工具，甚至可能推动其证明。

B.高效计算应用：可快速生成或筛选孪生素数，优化密码学、计算机科学等领域对大素数的需求。

C.可以揭示素数规律：若公式普适，可能隐含素数分布的新模式，深化对数学本质的理解。

D.方法论创新：或启发其他素数相关问题的构造性解法（如哥德巴赫猜想)。

（3）孪生素数构造式的分析与证明

对提出的构造式进行了理论分析，探讨了其能否覆盖所有可能的孪生素数对，或至少保证无穷性。关键点包括：

A.完备性：公式是否遗漏某些特殊形式的孪生素数；B.有效性：能否通过有限计算步骤验证其正确性；

C.与经典猜想的关联：如构造式隐含了素数分布规律，可能为猜想提供新视角。

(4)总结与展望

本文的“求任意两数间孪生素数的公式”为孪生素数研究提供了潜在的计算工具，但尚需进一步严格论证其数学完备性。未来方向可能包括：优化公式的计算效率，将其与筛法理论结合，或通过反例检验边界条件。若构造式被证实无误，或为孪生素数猜想的最终解决开辟新路径。下一章，我们将从宏观、微观以及宏微观相结合三个方面来证明孪生素数猜想。

附录1.参考文献：

A.经典理论与猜想

(1)Hardy, G. H., Littl ewood, J. E. (1923). Some problems of 'Partitio Numerorum'; III: On the expression of a number as a sum of primes. Acta Mathematica, 44, 1-70.

（哈代—李特尔伍德猜想，包含孪生素数分布的启发式分析）

(2) Brun, V. (1919). Le crible d' Eratosthène et le théoreme de Goldbach. Skr ifter Utgitt av Videnskapsselskapet i Kristiania, 3, 1-36. （布伦筛法，首次证明孪生素数倒数和收敛）

B.突破性进展

(3)Zhang, Y.(2014). Bounded gaps between primes. Annals of Mathematics, 179(3), 1121-1174.

（张益唐的里程碑工作，证明存在无穷多对素数间隔小于7000万）(4)Maynard, J. (2015). SmalI gaps between pr imes. Annals of Mathematics, 181(1), 383-413.

（梅纳德改进张益唐结果，将间隔缩小至600）

(5) Polymath8. (2014). Variants of the Selberg sieve, and bounded intervals containing many primes. Research in the Mathematical Sciences, 1(1),12.

（Polymath项目对素数间隔的集体优化成果）

C.计算方法与算法

(6 )Pritchard,  P. (1987).  Improved incremental prime number sieves. Algorithmica, 2， 247-262.

（改进的素数筛法，可用于高效生成孪生素数）

(7)0liveirae Silva, T., Herzog, S., & Pardi, S. (2014).

Empirical ver ification of the even Goldbach conjecture and computation of prime gaps up to 4×1018. Mathematics of Computation, 83(288)， 2033-2060.

（大范围素数计算与验证的实证研究）

D.理论分析与构造

(8) Green, B., Tao, T. (2008). The primes contain arbitrarily long arithmetic progressions. Annals of Mathematics, 167， 481-547.

（格林—陶定理，揭示素数分布的规律性）

(9) Soundararajan, K. (2007). Smal I gaps between pr ime numbers: The work of Goldston-Pintz-Yildirim. Bulletin of the American Mathematical Society, 44(1),1-18.

（素数间隔问题的综述，涵盖GPY筛法）

E.教材与综合参考

(10 Apostol, T. M. (1976). Introduction to Analytic Number Theory. Springer.

（解析数论经典教材，涵盖素数分布理论基础）