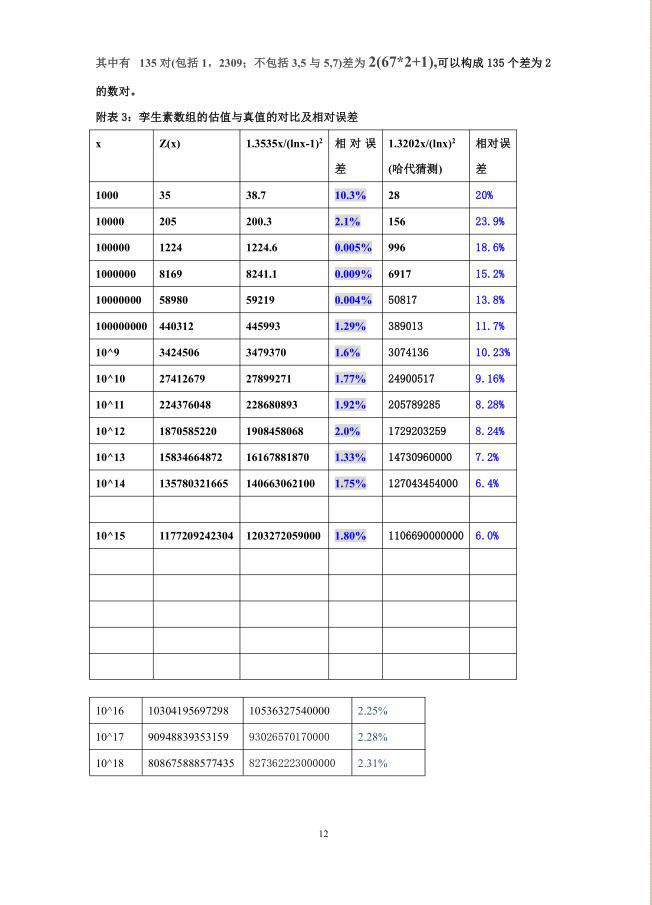
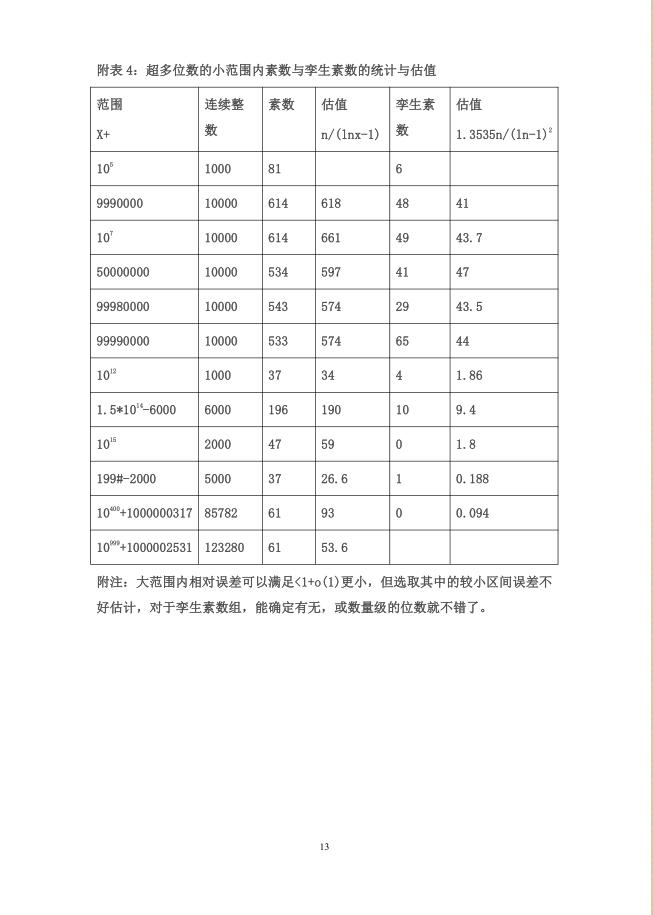
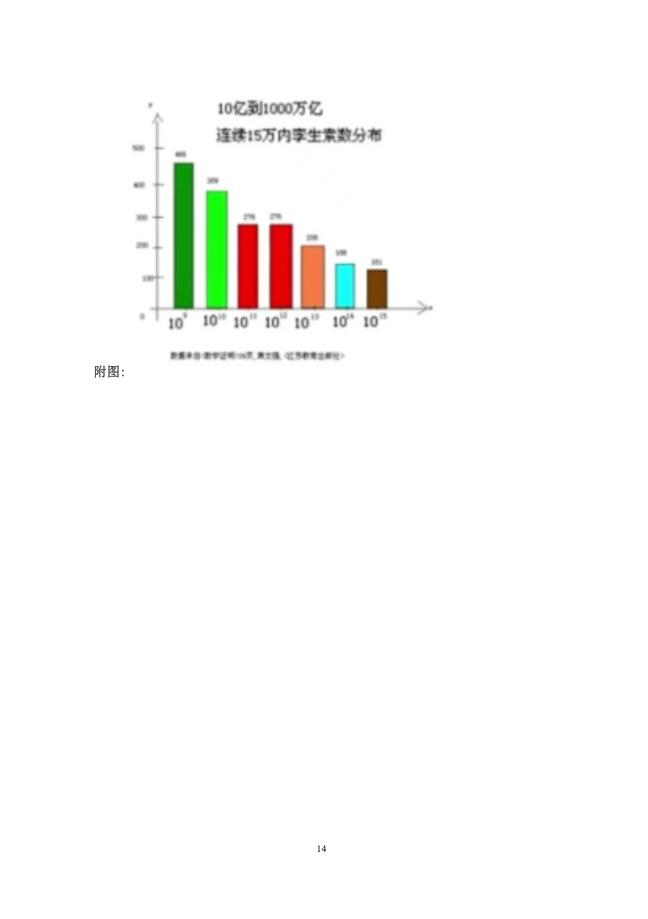
摘要：研究孪生素数组，自然从小到大，先从小范围找到规律，结合中国剩余定理，与埃斯特拉染尼氏筛法，逐步扩大到大范围验证，多次反复，依据两大素数定理，得出有理有据的估值公式（一元连续可导的初等函数关系式表示），再由“互联网+数论”的大数据给出令人信服的验证，从而用数学分析知识把范围推广到无穷大。

[关键词]素数，孪生素数，动态密度，缩剩余类，相对误差

[数学符号]：

Z₂(x)表示小于x的孪生素数组数

P#不大于p的素数的连乘积，例如7#=2*3*5*7=210

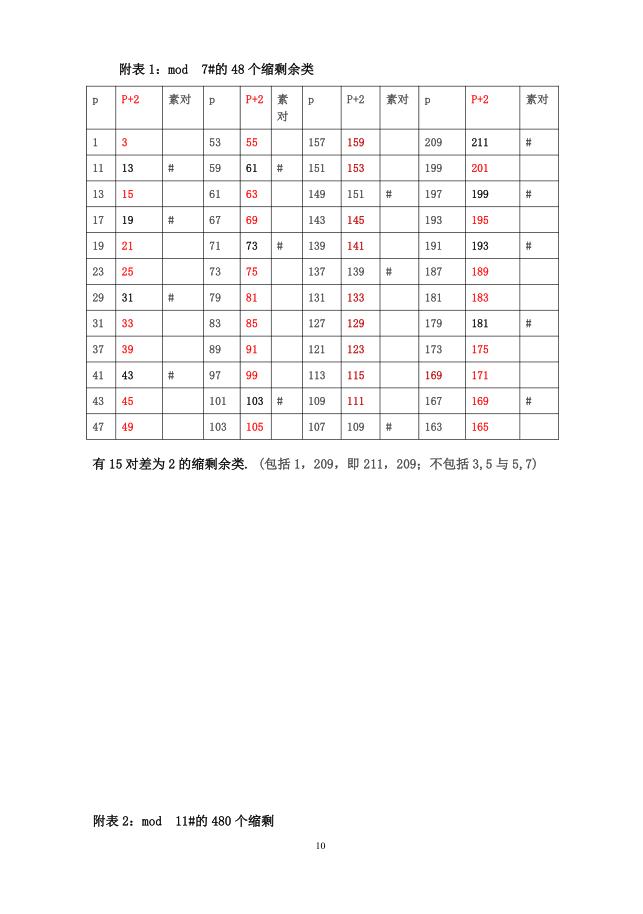
C 表示Z₂(x)对于连续可导的函数的偏离度。

o(1)小于1的量，本文特别限定-1/2<o(1)<1.

[x]     x的整数部分。

π（x）    素数分布函数，不超过x的素数个数。

π（x：6,1）、π（x：6,5）素数中模6的缩剩余类，φ(m)欧拉函数，不超过m且与m互素的正整数的个数，例如φ(6)=2

【中图分类号】N53           【文献标识码】A 

英文摘要

Abstract: Research on twin prime series, naturally from small to large, first find the law from a small range, combined with the Chinese remainder theorem, andratosthenes sieve method gradually expand to a large range of verification, multiple iterations,based on the two major prime number theorems, draw a well-founded valuation formulaelementary function relationship expressed in one variable continuous differentiable), and then by the "Internet number theory" The big data gives convincing verification, thus using mathematical analysis knowledge to generalize range to infinity.

[引言]

“李生素数有无穷多”的猜想，1849年由数学家波林那克提出，被数学家希尔伯特列为世界二十三个数学难题中的第八难题的一部分（1900年）

1922年，英国数学家哈代与李特伍德提出猜测：

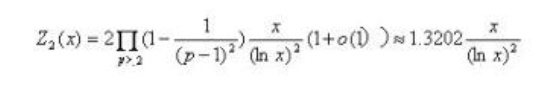
精确度不太高，可以改用优化后的素数分布公式。但公式的推导依赖素因子分解定理（至今无法彻底解决），这也是哈代承认整体成功而细节上失败的缘由.，如何绕过是最大难点.

（一）用动态密度估值时，modp#中p增大决定c→1.3202

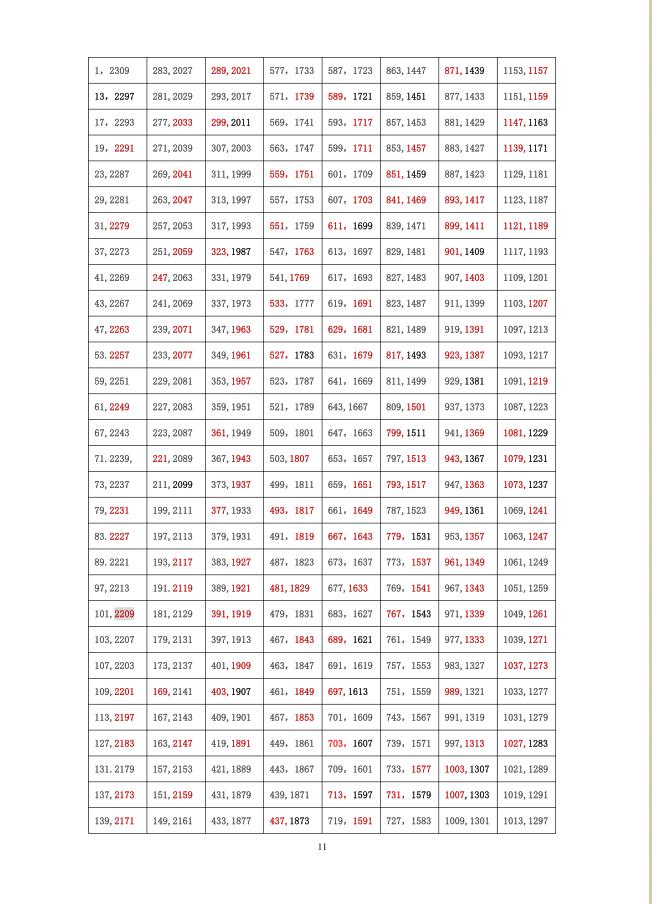
本人1993年在第二届全国初等数学研究学术交流会上提出的论文中猜测：

其中的系数=1.5基于把素数分为6n+1，6n—1两类，分别进行动态密度估值，“孪生素数猜想”，就是给定一个范围[1，x]，具体确定其中大约有多少对孪生素数，完成如下填括号 (    )=(    ) -2