摘要 完美长方体猜想提出已经有300多年了，人们试图通过各种方法找到它存在的事实，本文通过建立长方体的3条棱长、3条面对角线长和体对角线长之间的所有毕得哥拉斯型方程，再利用Brahmagupta-Fibonacci恒等式，我们发现当“棱长--面对角线长-体对角长”之间二连等方程存在“本原-本原”通解式时，但在3条棱长之间的毕得哥拉斯型方程中，至少有1个不存在毕得哥拉斯数解，因此，不存在同时满足长方体所有的毕得哥拉斯型方程的毕得哥拉斯数解，这样就证明了完美长方体是不存在的.

关健词:完美长方体猜想，欧拉砖，毕得哥拉斯型方程，本原毕得哥拉斯数，Brahmagupta-Fibonacci恒等式，连通解式

作者声明:本论文知识产权归作者所有，若有侵权，依法必究!

1.研究历史与进展

1.1 问题的由来

关于完美长方体问题(也被称为欧拉完美长方体问题)的介绍很多，但未查到有关公开的数学论文.这里介绍的是文[11中的部分相关内容:英国数学家约翰·里奇借助平面内完美正方形问题，提出了研究空间完美长方体问题，也叫有理长方体问题。

在介绍此问题时，许多人处于习惯考虑,称其为完美立方体问题,我们很容易证明完美正方体不存在.因此，为了保持数学上的严谨性应该称这个问题为完美长方体猜想。

这样完美长方体猜想的数学表述是:存在一种长方体，它的3条棱、3条面对角线、以及体对角线的长都是自然数.

约翰·里奇是当代数学家，可能是他先公开提出这个“完美长方体猜想”，同时也有人说这个猜想最早是丢番图提出的，应该也有很大可能性。还有人认为完美长方体猜想与费马大定理的提出过程类似可以推测早期的数学家也是受毕得哥拉斯定理和毕得哥拉斯数的启发，发现和提出了完美长方体猜想

但是，完美长方体猜想为什么没有被命名为某个人名猜想，又说明这个猜想可能被不同时代的不同人都个自独立发现过!

1.2研究历史与当前进展

1719年，德国工程师巴克发现了1种长方体,3条棱长分别为:a=117、b=44、c=240，那么有

a²+b²=117²+44²=125²

b²+c²= 44²+240²=244²

c²+a²=117²+240²=267²

a²+b²+c²=117²+44²+240² =73225

但73225不是平方数

在历史上，欧拉曾研究过完美长方体问题，如果研究其中只有1面对角线不是自然数的长方体问题，就把这个问题转化为了欧拉砖问题，也叫欧拉长方体.

欧拉也曾找到1个拟完美立长方体,3条棱长分别为:a=153b=104、c=672，那么有

a²+b²+c²=153²+104²+672²=697²

a2+b2=153²+104²=185²

b²+c²=104²+672²=680²

c²+a²=153²+672²=474993

但 474993 不是平方数.

欧拉后来专门研究了一下:怎样的3个数才能形成这种关系性质他找到了至少2组“参数化公式”，还可以算出巴克发现的长方体是体积最小的欧拉砖.

与欧拉同时代的英国数学家桑德森也发现了1个欧拉砖的通解公式，而且是以毕得哥拉斯数为基础构造的，假设(u,v,w)是一组毕达哥拉斯数，则有(lu(4v²-w²)|,v(u²-w²)|,4uvw )必为欧拉砖数,说明欧拉砖的组数是无穷的。

1895年，法国数学家布罗卡德曾声称，他证明不存在完美长方体。不过后来有数学家发现他的证明有误，

进入20世纪80年代以来，数学家利用计算机寻找完美长方体从 1985 年可能存在的最小棱数106,已经提高到了1000亿内的所有立方体，但仍未找到1个完美长方体.

据[2]介绍，有关完美长方体猜想的讨论研究很多，但还没有被人发现过，也没有人能证明它存不存在

时至今日，有人把完美长方体猜想与“转角沙发”等难题并列为“5小”世界数学难题

2.原猜想的丢番图方程表示和主要结论

根据前面提到的有关完美长方体猜想是:存在一种长方体，它的3 条棱、3 条面对角线、体对角线的长都是自然数。

我们继续设长方体的3条棱长为a,b,c,并设长方体的3条面对角线长为 x,y,，以及体对角线长为 w，如图所示:

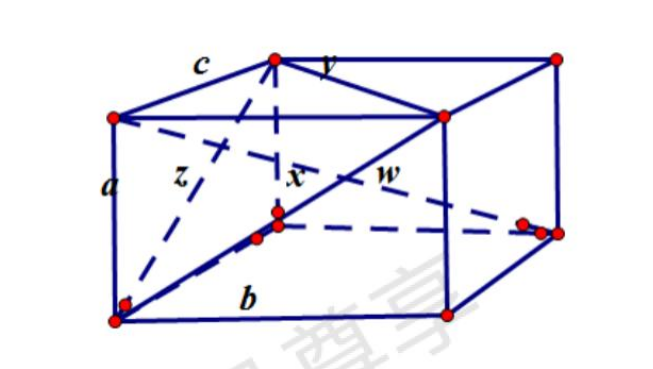
这样可以多次利用毕得哥拉斯定理,得到下列长方体所有的毕得哥拉斯型方程组:

a²+ b²=x²                    (2.1)

b² + c²= y²                      (2.2)

c²+a²=z²                        (2.3)

x² +c²= w²                    (2.4)

y²+a²=w²                        (2.5)

z² + b²= w²                    (2.6)

我们就建立了“完美长方体”关于3条棱长、3 条面对角线长和体对角线长之间所有关系的6个方程.这6个方程是1组7元2次(齐次)丢番图方程组，简称为G-6.

这样上述完美长方体猜想问题就转化为:求解同时满足所有G-6的毕得哥拉斯数解;或者，证明不存在同时满足所有G-6的毕得哥拉斯数解。

我们运用初等数论方法证明了:

定理    在 G-6 中，若方程(2.1)和(2.4)存在本原毕得哥拉斯数解,以及方程(2.4)、(2.5)和(2.6)存在“本原-本原”二连等通解时，但方程(2.1)、(2.2)和(2.3)中至少有1个不存在毕得哥拉斯数解.因此，不存在同时满足 G-6所有方程的毕得哥拉斯数解,

3.定义和若干引理

3.1与毕得哥拉斯型方程相关的定义和引理

定义1若正整数 A,B,C满足

A²+B²=C²            (3.1）

称方程(3.1)为毕得哥拉斯型方程，并称满足方程(3.1)的正整数解(A,B,C)为毕得哥拉斯数组.

若设 gcd(A,B)=d，即d为A和 B的一个大于1的整数因子.由方程(3.1)有d|C、故可取 d=1,则有 gcd(A,B)=1,其中A,B,C没有一个共同的因子，即 gcd(A,B,C)=1.这时满足方程(3.1)的正整数解(A,B,C)可称为本原毕得哥拉斯数。

引理 3.1在方程(3.1)中，若正整数解(A,B,C)为本原毕得哥拉斯数，则 gcd(A,B)=gcd(B,C)= gcd(C,A)=1.

证明 若方程(3.1)的正整数解(A,B,C)中,有两个是d(d ≥1)的倍数,则剩下一个也是 d的倍数，则有 gcd(A,B)= gcd(B,C)=gcd(C,A)= d，此时由于(A,B,C)为本原毕得哥拉斯数，则须 d=1.

显然，引理 3.1的逆命题也成立，则有下面结果:

引理 3.2 在方程(3.1)中，若(A,B,C)为毕得哥拉斯数组，且有gcd(A,B)=1，或者 gcd(B,C)=1，或者 gcd(C,A)=1，则(A,B, C)为本原毕得哥拉斯数

由引理 3.2 可知,在方程(3.1)的正整数解(A,B, C)中,若有 gcd(AB)=gcd(B,C)= gcd(C,A)=1 时，不失一般性，可设2|B 时,则有下面结果:

引理 3.3 若方程(3.1)的正整数解(A,B,C)为本原毕得哥拉斯数,全部正整数解可表示为

A=m²-n²,B=2mn,C=m²+n²

其中m>n，(m，n)=1，且m，n为奇偶性互异的正整数。

定义2     在引理 3.3 情况下，方程(3.1)的正整数解(A,B,C)的3个等式称为本原毕得哥拉斯数(A,B,C)的通解式，可简称为本原毕得哥拉斯数通解式.

在引理 3.3 情况下,方程(3.1)的正整数解(A,B,C)的3个等式也可以表示成下面的表达式

A=(m²-n²)t,B=2mnl, C=(m²+n²)t.

其中m>n，(m，n)=1，m，n为奇偶性互异的正整数，且t>1,t也为正整数。

定义3 这3个等式可以称为通用毕得哥拉斯数(A,B,C)的通解式，也可简称为通用毕得哥拉斯数通解式，

定义4为了方便后续的讨论分析，我们可将方程(3.1)中的本原毕得哥拉斯数 A、B 和C 分别为:A 位数、B 位数和C 位数.

因此，我们很容易得到引理 3.1的一个推论:

引理 3.4 在本原毕得哥拉斯数(A,B,C)中，则有 A 位数为奇数,B 位数为偶数，且 C位数为奇数.

3.2   与 G-6有关的若干引理

引理 3.5 在 G-6 中，方程(2.1)、(2.2)和(2.3)中的 a、b、c两两互不相等，

证明，这个结果可由毕得哥拉斯定理证明，否则在体对角线长x、y、z 中会存在无理数。

引理3.6在G-6中，由a、b、c的对称性，不妨设a<c，则可得到 a<x, b< x,且 x≠c;还有 c<y, c<z，且x<z<W.

证明 在 G-6中，利用毕得哥拉斯数的性质和方程(2.1)、(2.2)、(2.3)、(2.4)、(2.5)和(2.6)之间的代数关系，可以很容易证明此引理。

引理3.7在G-6中，若方程(2.1)存在本原毕得哥拉斯数解，则方程(2.4)也可以存在本原毕得哥拉斯数解.

证明 可以把方程(2.1)的解作为 G-6解的起始条件，不妨设方程(2.1)存在本原毕得哥拉斯数解.由于方程(2.1)、(2.2)和(2.3)是 a,b,c循环构建的毕得哥拉斯型方程组，在这3个方程中，至少有1个方程的各项都是偶数，它的解就不是本原毕得哥拉斯数。

实例验证:在巴克发现的长方体中,3条棱长分别为:a=117，b=44，c=240，那么有

y²=b²+c² == 》244²=44²+240²

z²=c²+b² ==》(89x3)²=(80x3)²+(39x3)²

在欧拉找到的拟完美立长方体中,3条棱长分别为:a=153、b=104、c=672，则有

y²=b²+c² ==》680²=104²+672²

另外，方程(2.4)中的x和c项不受方程(2.1)、(2.2)和(2.3)的毕得哥拉斯数循环解的限制，也可以存在本原毕得哥拉斯数解。

实例验证:在欧拉找到的拟完美立长方体中，则有

w²=x²+c²  ==》697²=185²+672²

根据引理 3.7，我们还可以得到一个推论:引理 3.8 在 G-6中，若方程(2.1)和(2.4)存在本原毕得哥拉斯数解，则方程(2.5)和(2.6)也可以存在本原毕得哥拉斯数解.证明在G-6中，由引理3.7易知

gcd(a, x)=gcd(x,w)=gcd(a, w)=1

以及

gcd(b,x=gcd(x,w)=gcd(b, w)=1

根据引理 3.2,方程(2.5)和(2.6)也可以存在本原毕得哥拉斯数解

3.3 Brahmagupta-Fibonacci恒等式与若干新引理

根据著名的 Brahmagupta-Fibonacci恒等式(婆罗摩笈多-斐波那契恒等式，也被称为丢番图平方和恒等式)，我们知道:任何两个数的平方和与另两个数的平方和的乘积，也仍然是两个数的平方和.

那么，可以获得下面若干重要结果:

引理3.9 若AB、C.D是两两互不相等的正整数，则有

N=A²+B²=C²+D²            (3.2)

那么,(3.2)式成立的充分必要条件是

N=(p²+q²)(r² +s²)          (3.3)

其中p，q，r,s都是正整数，且有p≠q，r≠s，pr≠gs ，ps≠qr

证明(1)先证明充分性.

设(3.2)式的中 p,q,r,s 都是正整数，且有 p≠q，r≠s，pr≠gs,ps≠qr.则有

N=p²r²+p²s²+q²r²+q²s²=(pr +qs)²+(ps-qr)²=(ps +qr)²+(pr-qs)²

可令A=pr+gs，B=|ps-gr|，C=ps+qr,D=|pr-qs|

则有N=A²+B²-C²+D²

因ps≠ar，pr≠as，则有B=lps-gr≠0，D=|pr-gs|≠0

因 B=|ps-qr|=±(ps-qr)，则有 A=pr+qs≠±(ps- qr)=B.

因p≠q，r≠s，则有(p-q)(r-s)≠0 ，pr-ps-qr+gs≠0则有 A=pr + qS ≠ps+qr=C

因p≠0，r≠0，pr主0，所以pr+gs≠(pr-qs);则有 A=pr+qs≠ |pr - qs|=D.

同理可证明 B≠C,B≠D 和C≠D

(2)再证明必要性.

设(3.2)式中的 A,B.C，D都是两两互不相等的正整数

首先，不可能发生: A,B都是偶数,而 C,D都是奇数;或 A,D 都是奇数，而C,D都是偶的情况，因为两个偶数平方和是4的倍数,而两个奇数平方和不是4的倍数。所以，在C,D中至少有一个与A奇偶相同，不妨设就是 D.于是有

因为 B=|ps-qr ≠0，所以 ps≠ qr.

同时，还有

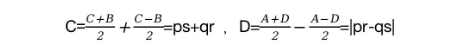
则有

N=C²+D²=(ps+qr)²+(pr-qs)²=p²r²+p²s²+q²r²+q²s²=(p²+q²)(r² +s²)

那么，可得到(3.3)式

同理可证得 p≠q，r≠s，pr≠ qs，ps≠qr

实例验证:若设 p=1，q=2,r=2,s=3.则有

N=8²+1²=7²+4²=(1²+2²)(2²+3²)

根据引理引理 3.9，可以得到毕得哥拉斯数组的一个有趣结果:

引理 3.10 任何2组毕得哥拉斯数的C位数C₁和C₂的乘积，也仍然是2组C位数相同的毕得哥拉斯数的C位数，若设这个C位数为C₃,则有 C₁C₂=C₃ 且C₁≠ C₂.

实例验证:若设C₁=5，C₂=13，且C₃=65.则有

65²=63²+16²=56²+33²

引理 3.11 若有丢番图方程

XY=Z²                    (3.4)

正整数 X Y满足 X>Y>1.

那么，方程(3.4)的正整数通解式有2种,1种为X=u² Y=v²，Z=uv.       (3.5)

其中 u,v都为正整数,且 gcd(u, v)=1

另1种为

X=kh²，Y=k，Z=kh.            (3.6)

其中k不是1个完全平方数,k>1,h>1，且 gcd(k,h)=1

证明要使2个正整数X和Y的乘积为1个完全平方数，则有3种情况: X=Y;X和Y都是完全平方数;X=kh²，Y=k，gcd(k, h)=1

其中有“X和丫都是平方数，以及 X>Y>1 ”符合方程(3.4)的条件，若设X=u²,Y=v²,则有Z=uv，且 gcd(u,v)=1.可得方程(3.4)的正整数通解式(3.5).

其中还有“X=kh²,Y=k，以及X>Y>1”也符合方程(3.4)的条件，若设X=kh²，Y=k，gcd(k,h)=1，则有 Z=kh.且 gcd(k,h)=1.可得方程(3.4)的正整数通解式(3.6).

根据引理 3.9 和引理 3.11，可得到:

引理 3.12 若(3.3)式中的N是1个完全平方数，可设N=W²

则有

W²=(p²+q²)(r² + s²)             (3.7)

那么，(3.7)式成立的充分必要条件是

p²+q²=u²，r²+s²=v²            (3.8)

其中 u>v,且(p, q,u)和(r,s,v)都为本原毕得哥拉斯数组,

证明(1)先证明充分性

这个结论很容易证明，可以把(3.8)式代入(3.9)式,可得

N= W²=(uv)²

则N是1个完全平方数，

(2)再证明必要性.

由于(3.7)式的左端为1个完全平方数，而右端可看成2个正整数的乘积，根据引理 3.9，有下面 2情况:

①若要使(3.7)式成立，根据引理 3.9的(3.5)式，右端2个正整数必须是2个完全平方数，那么(3.7)式的左端才能是1个完全平方数这就证明了(3.8)式的充分性.

②)若要使(3.7)式成立、根据引理3.9的(3.6)式，右端2个正整数必须有下面的关系式

p²+q²=h²(r²+s²)=(hr)²+(hs)²                (3.9)

其中h为正整数,且 h>1.则有

gcd(p, a)=gcd(hr, hs)=h                (3.10)

但(3.10)式与 gcd(p,q)=1矛盾,那么(3.9)式不成立，也就进一步证明了(3.8)式的充分性.

4.定理的证明

4.1新证明方法的发现

在研究欧拉发现的欧拉砖时，我们发现当a,b,c构建成毕得哥拉斯型方程(2.1)、(2.2)和(2.3)时，会出现 a,b,c在方程组中的循环关系.同时又要满足方程(2.4)、(2.5)和(2.6)存在毕得哥拉斯数解,还有更严格的要求是，方程(2.4)、(2.5)和(2.6)还是二连等的毕得哥拉斯型

方程.这样可以把方程(2.4)、(2.5)和(2.6)写成3个二连等的毕得哥拉斯型方程

w²=x²+c²=y²+a²

w²=y²+a² =x²+b²

w²=z²+b²=x² +c²

根据引理 3.7 和引理 3.8,方程(2.4)、(2.5)和(2.6)都存在本原毕得哥拉斯数解.这3个二连等的毕得哥拉斯型方程可能存在二连等的本原毕得哥拉斯数通解式，可简称为“本原-本原"通解式,

实例验证:在欧拉找到的拟完美立长方体中，则存在“本原-本原"等式

697²=185²+672²=680²+135²

根据引理 3.9、引理 3.10 和引理 3.11，以及方便后续的定理证明，可以把这3个二连等的毕得哥拉斯型方程变换成同类更一般的一连等毕得哥拉斯型方程

W²=A²+B²=C²+D²                (4.1)

我们将找到方程(4.1)的“本原-本原"通解式等结果，再进一步利用这些结果，完成对定理的全部证明.

引理 4.1 当方程(4.1)存在正整数解时，其“本原-本原"通解式为

根据引理 3.10和引理3.12，此时还有W=uv，充分证明W是2组C位数相同的毕得哥拉斯数的C位数.

根据引理 3.9 和引理 3.12，可得到“本原-本原"通解式

W²=A²+B²=C²+D²=(p²+q²)(r² + s²)

以及

A=pr+qs，B=|ps-qr|，C=ps+qr, D=|pr-gs|.

其中 p，q，r，s都是正整数，且p≠q，r≠s，pr≠qs，ps≠qr.

引理 4.2 在方程(4.1)的“本原-本原"通解式中，则有(A,B,W)和(C,D,W)为本原毕得哥拉斯数.

证明 根据方程(4.1)的“本原-本原"通解式，假设 gcd(p,r)=m,m> 1, p=mp', r=mr'.则有

A=pr+qs=m²p'r'+qs ,B=|ps-qr|=m(|p's-qr'|)

若有 gcd(q, s)=m，则有 gcd(pr, qs)=m, gcd(p, q)=gcd(r, s)=m.与 gcd(p, q)=gcd(r, s)=1 矛盾.则有 gcd(A, B)=1.

假设 gcd(p, s)=n,n >1.同理可证，则有 gcd(p, q)=gcd(r, s)=n也存在矛盾。则有 gcd(A,B)=1.

同理可证,gcd(C,D)=1.那么方程(4.2)的正整数解(A, B, W)和(C,D,W)则为本原毕得哥拉斯数,

实例验证:当 p=3,q=4; r=5,s=12 时，则有

A=63,B=16;C=56,D=33

以及“本原-本原”二连等式

65²=63²+16²=56²+33²

4.2 定理证明

根据前面的分析讨论易知，在 G-6 中，由方程(2.4)、(2.5)和(2.6)可以构造出更一般的二连等毕得哥拉斯型方程(4.1).并由引理 4.1和引理 4.2 给出了方程(4.1)的“本原-本原"通解式.

下面我们将进一步证明:

当方程(4.1)存在“本原-本原"通解时，在下列4个毕得哥拉斯型方程

X²=A²+C²            (4.3)

Y²= A² + D²        (4.4)

Z²=B²+C²            (4.5)

U² = B² + D²        (4.6)

中，不存在满足方程(2.1)、(2.2)和(2.3)其中之一的毕得哥拉斯数解,(1)由方程(4.1)的“本原-本原"通解式可得

X²=A² +C²=(pr+ qs)² + (ps + qr)²=(p²+q²)(r² + s²)+4pqrs

则有

X²=W²+4pqrs            (4.7)

由此可知，当4pgrs为1个完全平方数时，虽然方程(4.7)可能有毕得哥拉斯数解，但 X> W,这与引理 3.6 矛盾。

因此，方程(4.7)不存在满足 G-7 中所有方程的正整数解.(2)由方程(4.1)的“本原-本原"通解式可得

Y²=A²+D²=(pr+qs)²+(pr-qs)²=2[(pr)²+(qs)²]

此时，设 Y=2Y',A'-pS, D'=qr，可得

2Y2=A2+D2            (4.8)

据[3]介绍，方程(4.8)存在正整数解，则有

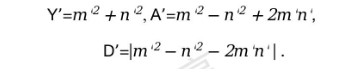
这里 m',n'为正整数,且有 m'>n'.

可得方程(4.4)的正整数解，则有

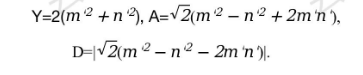
但方程(4.4)的正整数解,不是方程(2.1)、(2.2)和(2.3)其中之一所需的毕得哥拉斯数解.

(3)由(4.1)的“本原-本原"通解式可得

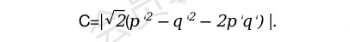
但方程(4.5)的正整数解，不是方程(2.1)、(2.2)和(2.3)其中之一所需的毕得哥拉斯数解

(3)由方程(4.1)的“本原-本原"通解式可得

U²=B²+D²=(ps-qr)² +(pr-qs)²=(p²+q²)(r²+s²)-4pgrs=w²-4pgrs

则有

U²+4pgrs=W²            (4.10)

当 4pgrs 可能为1个完全平方数时，方程(4.10)也存在毕得哥拉斯数解,但 C 位数则是 W，而不是满足方程(2.1)、(2.2)和(2.3)其中之所需的毕得哥拉斯数解.

根据上述4种情况的分析讨论的结果,我们可以得到:在G-6中，当方程(2.5)(2.4)、(2.5)和(2.6)存在“本原-本原”通解时，但方程(2.1)、(2.2)和(2.3)中至少有1个不存在毕得哥拉斯数解.从而证明了:不存在同时满足所有 G-6方程的毕得哥拉斯数解:定理证毕!

4.5 总结

我们通过建立长方体的3条棱长、3条面对角线长和体对角线长之间的毕得哥拉斯型丢番图方程，再利用Brahmagupta-Fibonacci恒等式，发现“棱长--面对角线长--体对角长”之间的二连等方程存在“本原-本原”通解式，但在3条棱长之间的毕得哥拉斯型丢番图方程中，至少有1个不存在毕得哥拉斯数解,

因此，不存在同时满足所有G-6的毕得哥拉斯数解。这样证明了完美长方体是不存在的.

我们就完全解决了完美长方体猜想--这个世界数学难题!

参考文献:

[1]陈雪、黎渝 合著.《奥妙无穷的黄金分割》[M.北京:人民邮电出版社出版，第 113--114 页

[2][美]萨蒂扬·莱纳斯·德瓦道斯,马修·哈维著,刘巍然泽.魔法数学:16个数学未解之谜.[M].北京:民主与建设出版社,2021年8月第1版,第105--107页

[3]管训贵 编著.初等数论.[M1.安徽:中国科学技术大学出版,2022年2月第三版、第 98 页。

[作者声明:本论文知识产权归作者所有，若有侵权，依法必究!]