观察下表:

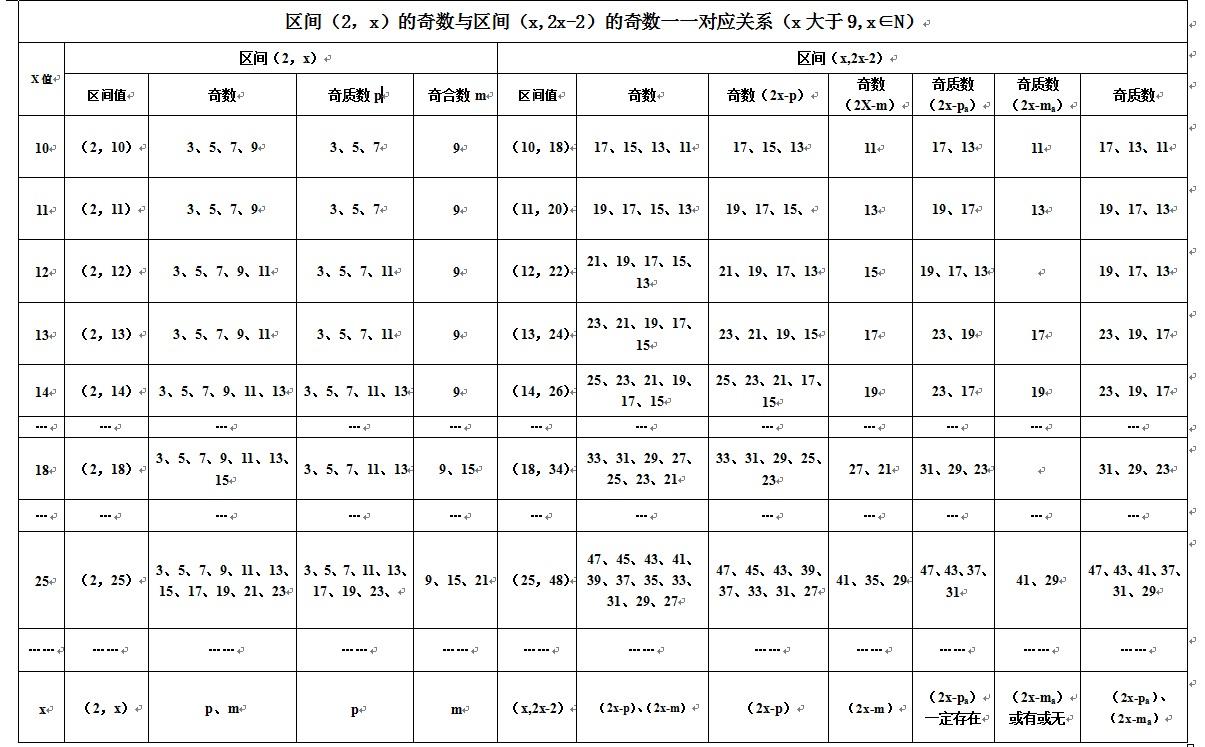
说明：p是小于x的奇质数, pa是使奇数（2x-p）为奇质数时的p，pa∈P。m是小于x的奇合数, ma是使(2ⅹ-m)为奇质数的m，ma∈M。

通过观察，容易发现：

1、区间（2，x）中的奇数只有奇质数p、奇合数m。(x>9,x∈N).

2、  区间（x，2x-2）中的奇数只有奇数（2x-p）、奇数(2ⅹ-m)。 (x>9,x∈N)。

3、 奇质数(2x-ma)在(x，2x-2)中，或存在或或不存在。[x>9,x∈N, m是小于x的奇合数,ma是使(2ⅹ-m)为奇质数的m]

4、奇质数(2x-pa)在(x，2x-2)中，一定存在。[x>9,x∈N, p是小于x的奇质数, pa是使(2ⅹ-p)为奇质数的p]

这些结论成立吗？

 伯特兰-切毕雪夫数学定理:

“若整数n > 3，则至少存在一个质数p，符合n < p < 2n − 2。”

因为这里“n > 3”，“n < p”，所以“质数p”一定是奇质数，因此，伯特兰-切毕雪夫数学定理可以表述为：“在区间(x，2x-2)中至少存在一个奇质数.(x>3，x∈N)”，或者，“在区间(x，2x-2)中一定存在奇质数.(x＞3，x∈N)”。

设a、x,使x＞9，a在区间(0，x)中 ,a∈N，x∈N。设b，使b在区间(x，2x)中，b∈N。

∵a在区间(0，x)中，

∴0＜a＜x ,

∴-ⅹ<-a<0，

∴-ⅹ+2x<-a+2x<0+2ⅹ，

∴x<-a+2x<2x，

∵b在区间(x，2x)中，

∴x＜b＜2x ,

又∵x<-a+2x<2x，

∴b=-α+2x.

当x一定时，α的个数一定，（-α+2x）的个数也一定，即 (2x-a)的个数也一定,b的个数也一定，而且，b是关于a的一次函数，

∵-1<0，

∴b是关于a的减函数。

即（2x-a）是关于a的一次函数，而且是减函数。

∴当x一定时，区间（0，x）中自然数a与区间（x，2x）中的自然数（2x-a）一一对应，而且二者具有负相关的关系,（2x-a）随着a的增大（或减小）而减小（或增大）。（x＞9，x∈N）(引理1)

∵x＞9，x∈N，

∴一定存在比x小的奇质数.

设p是小于x的奇质数，

∵x＞9，x∈N，

∴2x＞18，2x是偶数，

∵p是小于x的奇质数，

∴p是奇数。

又∵2x是偶数，

∴(2x-p)一定是奇数。

∵x＞9，x∈N，

∴一定存在小于x的奇合数.

设m是小于x的奇合数.

∵m是奇合数，

∴m一定是奇数，

∵2x>18，2x是偶数，

又∵m一定是奇数，

∴(2x-m)一定是奇数。

∵m是小于x的奇合数，

 奇合数≥9，

∴9≤m<ⅹ，

也就是，8<m<x(x>9，x∈N)。

又∵当x一定时，区间（0，x）中自然数a与区间（x，2x）中的自然数（2x-a）一一对应，而且二者具有负相关的关系(x>9,x∈N)，

∴x<(2x-m)<2ⅹ-8(x＞9，x∈N，m是小于ⅹ的奇合数)，

∴(2x-m)取值区间是(x，2ⅹ-8)(x＞9，x∈N，m是小于ⅹ的奇合数)。

∵除1外的奇数分为奇质数、奇合数两类，

∴大于2的奇数分为奇质数、奇合数两类，

∴区间（2，+∞）的奇数分为奇质数、奇合数两类，

∵区间（2，x）(x>9，x∈N)是区间（2，+∞）的一部分，

∴区间（2，x）(x>9，x∈N)中的奇数也分为奇质数、奇合数两类，

即

区间（2，x）(x>9，x∈N) (x>9，x∈N)中的奇数分为大于2、小于x的奇质数和大于2、小于x的奇合数两类，

∵p是小于x的奇质数，

 奇质数大于2，

∴p是大于2、小于x的奇质数，

∵m是小于x的奇合数，

 奇合数>2，

∴m是大于2、小于x的奇合数，

∵p是大于2、小于x的奇质数，

 m是大于2、小于x的奇合数，

  区间（2，x）(x>9，x∈N)中的奇数分为大于2、小于x的奇质数和大于2、小于x的奇合数两类，

∴区间（2，x）中的奇数只有p、m(x>9，x∈N). (引理2)

又∵当x一定时，区间（0，x）中自然数a与区间（x，2x）中的自然数（2x-a）一一对应，而且二者具有负相关的关系(x>9,x∈N)，

  区间(2，ⅹ)是区间(0，ⅹ)的一部分(x>9，x∈N)，

∴ 区间(2，x）中的奇数p、m分别与区间（x，2x-2)中的奇数（2x-p）、(2ⅹ-m)一一对应(x>9，x∈N)

又∵区间（2，x）中的奇数只有p、m(x>9，x∈N)，

∴区间（x，2x-2）中的奇数只有（2x-p）、(2ⅹ-m)(x>9，x∈N)。(引理3)

∵ⅹ>9>3，x∈N，

  在区间(x，2x-2)中一定存在奇质数(x＞3，x∈N)。

∴在区间(x，2x-2)中一定存在奇质数(x＞9，x∈N)。(伯特兰-切毕雪夫数学定理) (引理4)

又∵奇质数由奇数产生，

∴区间(x，2x-2)中的奇质数一定由区间(x，2x-2)中的奇数产生(x＞9，x∈N)。

又∵区间（x，2x-2）中的奇数只有（2x-p）、(2ⅹ-m)(x>9，x∈N)，

∴区间(x，2x-2)中的奇质数只能由奇数（2x-p）、(2ⅹ-m)产生(x＞9，x∈N)。

∵在区间(x，2x-2)中一定存在奇质数(x＞9，x∈N)，

  (2x-m)取值区间是(x，2ⅹ-8)(x＞9，x∈N，m是小于ⅹ的奇合数)，

∴(2x-m) 在区间(x，2x-2)中不一定存在奇质数(x＞9，x∈N)，

∴在区间(ⅹ，2ⅹ-2)中，奇质数(2x-ma）或有或无. [x＞9，x∈N，m是小于ⅹ的奇合数，ma是使(2ⅹ-p)为奇质数的m，ma∈M]。(引理5)

∵  在区间(x，2x-2)中一定存在奇质数(x＞9，x∈N)，(引理4)

   区间(x，2x-2)中的奇质数只能由奇数（2x-p）、(2ⅹ-m)产生(x＞9，x∈N)，

   奇数(2x-m）在区间(ⅹ，2ⅹ-2)中，不一定存在奇质数(x＞9，x∈N，m是小于ⅹ的奇合数)，

∴  奇数（2x-p）在区间(ⅹ，2ⅹ-2)中，一定存在奇质数(x＞9，x∈N)，

∴在区间(ⅹ，2ⅹ-2)中一定存在奇质数(2ⅹ-pa)。[x＞9，x∈N，p是小于ⅹ的奇质数， pa是使(2ⅹ-p)为奇质数的p，pa∈P]

容易验证，在区间(ⅹ，2ⅹ-2)中一定存在奇质数(2ⅹ-pa)。[3<x<10，x∈N，p是小于ⅹ的奇质数， pa是使(2ⅹ-p)为奇质数的p，pa∈P]

∴在区间(ⅹ，2ⅹ-2)中一定存在奇质数(2ⅹ-pa)。[x＞3，x∈N，p是小于ⅹ的奇质数， pa是使(2ⅹ-p)为奇质数的p，pa∈P] [奇质数(2ⅹ-pa)定理]

由此可知，“在区间(ⅹ，2ⅹ-2)一定存在奇质数(x＞3，x∈N，p是小于ⅹ的奇质数)”，是由于“在区间(ⅹ，2ⅹ-2)中一定存在奇质数(2ⅹ-pa)， [x＞3，x∈N，p是小于ⅹ的奇质数， pa是使(2ⅹ-p)为奇质数的p，pa∈P)]”。因此，伯特兰-切毕雪夫数学定理成立的根本，就是“在区间(ⅹ，2ⅹ-2)中一定存在奇质数(2ⅹ-pa)。 [x＞3，x∈N，p是小于ⅹ的奇质数， pa是使(2ⅹ-p)为奇质数的p，pa∈P]”。简言之，

伯特兰-切毕雪夫数学定理的本质，是奇质数(2ⅹ-pa)定理。

∵ p是小于ⅹ的奇质数，

  pa是使(2ⅹ-p)为奇质数的p，

∴ pa是奇质数，

∵2x= pa +(2ⅹ-pa)，

  pa是奇质数，

 (2ⅹ-pa)是奇质数，

∴2x可以表示成两个奇质数之和的形式。(x＞3，x∈N)

∵x＞3，x∈N，

∴2x＞6，2x是偶数，

又∵2x可以表示成两个奇质数之和的形式，(x＞3，x∈N)

∴大于6的偶数可以表示成两个奇质数之和的形式。

又∵6=3+3，3是奇质数，

4=2+2，2是质数，

∴≥4的偶数可以表示成两个质数之和的形式。

∴大于2的偶数可以表示成两个质数之和的形式。

这就是1742年德国数学家哥德巴赫提出的猜想。