同一律是数学理论在定义、推理和证明过程中必须要遵循的逻辑推理基本规则。

一、同一律

同一律（The Law Of Identity）是指一个数学理论在定义、推理和证明过程中，所使用的数学概念必须要始终保持同一，同一律可用公式表示为：A=A   也就是说，无论一个数学概念被使用或重复多少次，这个数学概念的内涵和外延必须是确定的，这样才能保证数学理论的确定性和无矛盾性。

如果在同一定义、推理和证明过程中，把两个完全不同的数学概念当作同一概念等同使用，或用一个完全不同的概念去代替原有的概念进行推理和证明，就会违反同一律，犯“混淆概念”或“偷换概念”的逻辑错误，破坏数学理论的逻辑完备性和客观真理性，出现逻辑上不能自洽和理论与经验事实不符等反常问题。

二、牛顿违反同一律引发第二次数学危机

x≠0 和 x=0是两个完全不同的数学概念。

牛顿在创立《微积分》时违反同一律，将 x≠0 和 x=0这两个不同的概念等同使用或相互代替，产生了著名的“贝克莱悖论”，引发了一场数学史上持续150年的第二次数学危机，《微积分》理论险被推翻。

英国大主教贝克莱（Berkeley）严厉批评牛顿是有意识地“混淆概念”，《微积分》理论是“分明的诡辩”，并指出“逻辑错误不会产生科学”。

整个18世纪，数学家们的首要任务就是消除《微积分》中的违反同一律逻辑错误，几乎每一位数学家都为此做出了巨大的努力。

后来柯西（Cauchy）将极限概念作为《微积分》的理论基础，才彻底消除了《微积分》中违反同一律的逻辑错误和“贝克莱悖论”，解除了数学史上的第二次危机。

三、《随机过程》是如何违反同一律的

根据《随机过程》教科书中的随机过程定义，“随机变量”和“样本函数”是两个内涵与外延完全不同的数学基本概念。

“随机变量”和“样本函数”描述的也是完全不同的实际问题或物理现象（图1）。对于布朗运动，“样本函数”用来描述一个布朗粒子的位移与时间之间的函数关系，“随机变量”则用来刻画所有布朗粒子在某一时刻的空间位置分布状态。

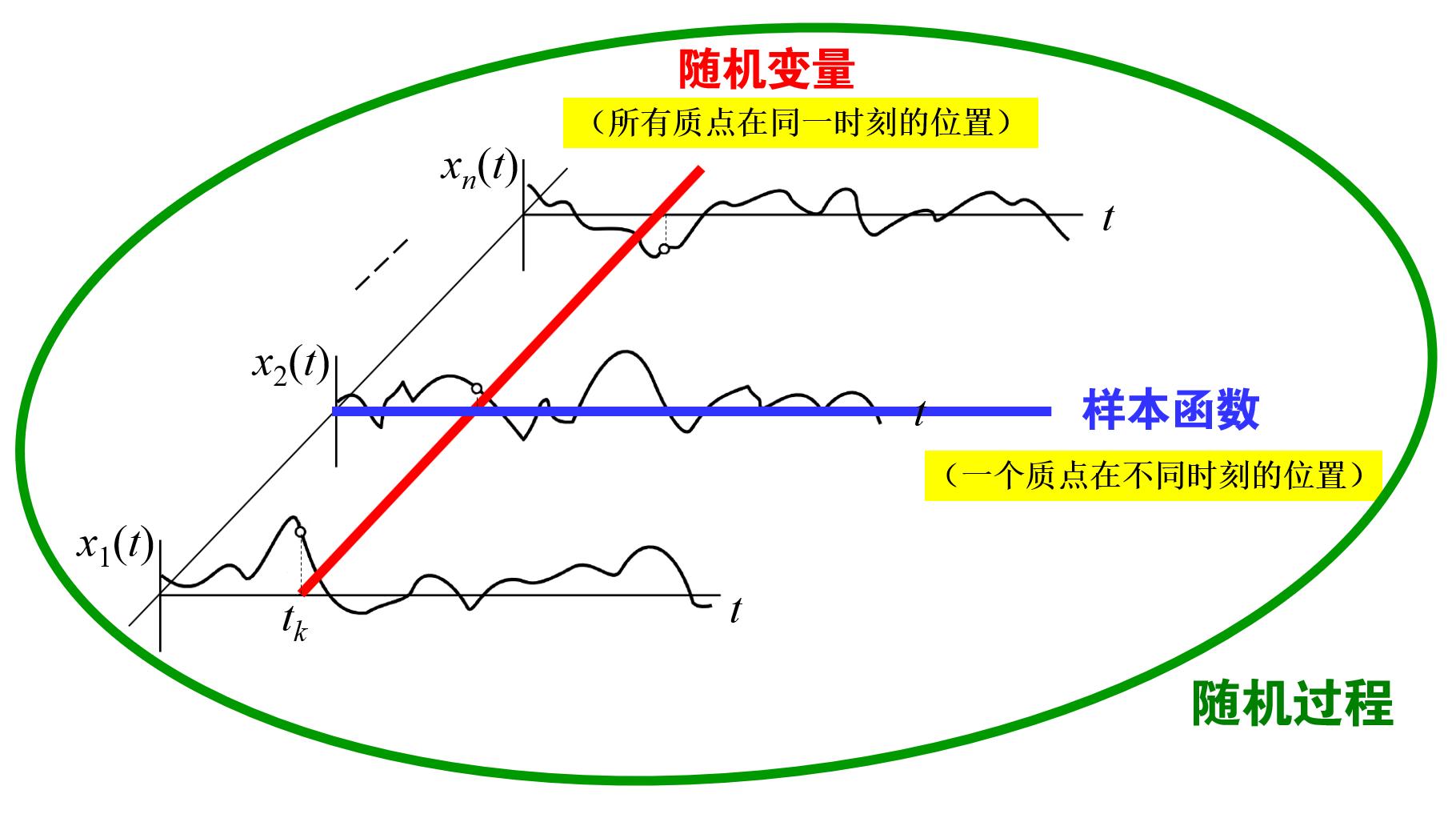
图1 随机过程、随机变量和样本函数的关系

自然科学、工程技术和社会科学领域大量的实验观测结果表明：布朗运动“随机变量”服从正态分布；布朗运动“样本函数”为不服从正态分布、功率谱密度与频率平方成反比的红噪声（Red Noise）；布朗运动“样本函数”的瞬时速度（导数）为白噪声（White Noise）。

以布朗运动定义为例，说明《随机过程》如何在同一个定义中违反同一律，产生了“混淆概念”逻辑错误。

《随机过程》教科书中是这样定义布朗运动的：

设X(t)为一个布朗粒子在t时刻的位移，X(0)=0，若

（1）X(t)为平稳独立增量过程；

（2）对于任意的t≥0，X(t)～N(0，σ2 (t))，其中σ>0为常数；

（3）X(t)是t的连续函数。

则称X(t)是布朗运动或维纳过程。

定义是通过简明陈述来揭示概念内涵的逻辑方法，定义通过“定义项”指出“被定义项（概念）”所反映事物的本质属性或数量关系来明确概念的内涵。

我们对上述布朗运动定义中的“被定义项”和三个“定义项”逐项进行分析：

被定义项X(t)为“一个布朗粒子在t时刻的位移”，显然，X(t)是随机过程X(ω,t)固定ω时的一个样本函数；

定义项（1）指出：被定义项X(t)是平稳独立增量过程X(ω,t)固定t时的随机变量；

定义项（2）指出：被定义项X(t)是服从正态分布的随机变量；

定义项（3）指出：被定义项X(t)是连续样本函数。

显然，从逻辑学的角度看，布朗运动定义中的“定义项”不仅没有保持与“被定义项”的概念同一，而且在“定义项”中用两个完全不同的概念描述“被定义项”，因此，布朗运动定义严重违反同一律，产生了“混淆概念”和“偷换概念”的逻辑错误。

总之，《随机过程》教科书中违反同一律的逻辑错误有以下三种表现形式：

（1）将“随机变量X(t)”和“样本函数X(t)”这两个完全不同的数学概念等同使用；

（2）用“随机变量X(t)”代替“样本函数X(t)”；

（3）用“随机变量X(t)”的性质（服从正态分布）代替“样本函数X(t)”的性质（不服从正态分布）。

因此，《随机过程》布朗运动理论完全建立在错误的“样本函数服从正态分布”基本假设基础上，并推导出了“布朗运动瞬时速度不存在（路径处处不可导）”这一与科学事实相悖的谬误。

四、结论

《随机过程》教科书违反同一律的逻辑错误导致布朗运动基本假设及逻辑结论均与科学事实不符，无法正确描述布朗运动现象及规律，为自然科学、工程技术和社会科学解决实际问题提供了错误的理论、方法及工具。