迈克尔阿蒂亚的黎曼猜想“证明”出来了。迈克尔阿蒂亚的证明错误百出。阿蒂亚的证明只有短短的五页纸！其中证明只有15行！可真的有那么简单吗？阿蒂亚在第二节定义的TODD函数就不靠谱，而这恰恰是证明的关键所在。

阿蒂亚是用了一个TODD函数的公式，假定有与黎曼猜想矛盾的点存在，这个公式是收缩的，那么就可以把一个个点代入这个公式，如果没有一个点成立，那么他就证明了黎曼公式。第一，阿蒂亚的“证明”在形式上也是错误的，根据演绎推理的逻辑规则：1，在两个否定的前提中不能得出结论,2，如果大前提是特称判断，小前提是否定判断，不能得出结论。3,前提中有一个是否定判断结论必须是否定判断。4，前提中有一个是特称判断结论只能是特称判断。5，......。阿蒂亚企图证明：大前提：有一个否定黎曼猜想的点存在（特称否定判断）。

小前提：这个点不存在（否定判断）结论：黎曼猜想成立。（全称肯定判断）阿蒂亚的企图违反了上面所说的逻辑规则。结论无论如何都得不出一个全称肯定判断。  第二，  错误在——假定。

1，假定。只能用在否定结果的证明中，例如，欧几里得证明素数无穷多个；或者费马无穷递降法。    假定a成立，可以推出b，得到c，c与a矛盾，所以假定的a不能成立，得到非a。

2，假定不能用在肯定的结论。假定a，可以推出b，得到c，c包含a，所以假定的a成立。（这个就是预期理由的错误）

3，为什么“假定”只能用于否定的结论，而不能用于肯定的结论？

 一个对科学理论更强的逻辑制约因素是，它们是能够被证伪的。换一句话说，因为以后能够被观测作有意义的检验，理论一定有被证伪的可能性。这种证伪的判据是区分科学与伪科学的一种方法。原因在于证实的内在局限性，证实只能增加一个理论的可信度，却不能证明整个理论的完全正确。因为在未来的某一个时刻，总是会发现与理论有冲突的事例。

现在我们问：阿蒂亚是证明了黎曼猜想是否成立呢？

1，阿蒂亚证明黎曼猜想成立。就是说他假设的那个“点”被自己证明没有，假设是建立在预期理由上，又被证明者否定，就是说前提不是真实的，违反逻辑规则——前提必须真实的原则。

2，阿蒂亚证明了黎曼猜想不成立，就是有那一个“点”存在，就是说阿蒂亚找到了反例，那么根本不需要什么在证明，指出反例就可以了。可是，阿蒂亚没有找到反例。

一，什么是黎曼猜想    黎曼猜想由数学家波恩哈德·黎曼（18261866）于1859年提出。它是数学中一个重要而又著名的未解决的问题。多年来它吸引了许多出色的数学家为之绞尽脑汁。克雷数学研究所以100万美元奖励证明黎曼猜想的人。

黎曼猜想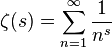：        主项：所有的非平凡零点     1，普遍概念和单独概念    世界上没有一个数学定理的主项是集合概念，所有的数学定理的主项都是普遍概念或者单独概念。

具有这种性质的元素：1，都属于这种事物。2，有多少数量”的判断。 例如勾股定理公式，椭圆公式，....。    2，集合概念命题的公式。

“某个事物（某个形式）的所有元素或者多个元素具有某种性质” 的判断。并且，黎曼猜想的每一个“零点”的S=X+Yi中的虚部Y值都是不同的的值都是素数。对于前几个自然数n = 0, 1, 2, 3...，多项式的值是41, 43, 47, 53, 61, 71...。当n等于40时，多项式的值是1681=41×41，是一个合数。实际上，当n能被41整除的时候，P(n)也能被41整除，因而是合数.。

集合概念的公式不能保证计算结果具有这个公式想要的结果性质，是一种不确定的结果公式。因为集合概念的每一个个体不是必然具有这个概念的基本属性。我们知道，黎曼猜想的每一个“零点”的S=X+Yi中的虚部Y值都是不同的。这个公式是一种形式上的集合，就是全部具备这种形式。

四，黎曼猜想是一个二阶逻辑问题，无法得到完整证明    黎曼猜想的 “零点” 也是一个集合，零点是这个对象上的函数，按照通常数学中定义，一个n元函数就是从论域A的个体的所有n元组的集合至A的一个映射。当我们用“所有个体”“存在个体”，量词加在论域的个体上，称为一阶量词。“    ” 所有函数”，“存在函数”，“所有关系”，“存在关系”是二阶量词，即二阶逻辑。黎曼所说的“所有零点”就是“所有函数”的二阶量词。    逻辑语言中的定理表示的是一个公式集合，并且该公式集合中的每一个公式都代表着知识的一个片段，由此我们可以给定理一个更准确的表达（这里所说的定理指的是在一阶逻辑中的定理，通常来说任意一个命题集合往往不一定是定理）。一阶逻辑可分成两个主要的部分：语法决定哪些符号的组合是一阶逻辑内的合法表示式，而语义则决定这些表示式之前的意思    因为数学只能处理最低级的无穷，不能处理更加大的无穷，看到了康托尔的厉害了吗？他认为无穷是有级别的。还因为证实的局限性，证实只能增加一个可信度，却不能证明理论完全正确。

五，数论中的猜想是不可靠的。

六，一个词项是属于什么类型的概念，取决于当时的语境。例如：1，黎曼猜想是一个著名问题。    这一句话中的“黎曼猜想”是一个单独概念。

七，以往的证明都是错误的    在证明黎曼猜想的历史中，美国莱文生1974年宣称证明“至少”有34%的零点成立是荒唐的，这是一个特称判断，说明莱文生证明必然错误，并且在集合概念前面加数量词34%，也是一种语法错误。  一个笑话：“小张经过一年努力掌握了1000多个英语词汇”。词汇是集合概念，表示一种语言词项的总汇，前面不能用“1000多个”限制。