1、全体自然数倒数的平方和。

大约从十七世纪开始，西方的数学家们终于打破了对于无穷的禁忌，逐渐应用无穷级数作为表示数量的工具，同时研究各种无穷级数的求和问题。1673年莱布尼茨去巴黎办事，顺便帮助惠更斯证明了 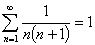，由此不仅导致了他与牛顿一起发明了微积分，而且还一并给出了下面二个无穷级数的和： 。

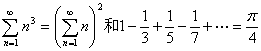前一个公式，我国元初时期的朱世杰，在他的《四元玉鉴》（1303年）一书中就已经给出。后一个公式，则是通过他的变换规则的方法所得到，显然这样的表示有些不妥，因为不管多少个有理数的和差，必定仍然为有理数，决不可能得到的是无理数，更不可能得到的是超越数。然而，那时真正困扰着莱布尼茨的却是调和级数的问题。

雅各布·伯努利严格证明了调和级数的发散性，即全体自然数的倒数之和为无穷大，但是雅各布·伯努利却被全体自然数倒数的平方和所困扰着。此后的欧拉应该是受到了莱布尼茨上述不妥的影响，于1735年先后给出了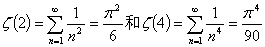： 。对于上述ζ（s）符号来说，当s为大于1的整数时，称为欧拉函数，当s为复数时，则称为黎曼函数。徐利治和郑毓信所写的《关系映射反演原则及应用》，对于ζ（2）的推导作了如下的介绍：

“由于 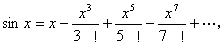于是sinx便可以看成是一个无限次的代数多项式。欧拉把它和代数多项式因子分解定理作比较，便联想到sinx也应该能表示成因子连乘积。因为sinx=0有无穷多个根：x=0，±π，±2π，±3π，……，所以sinx应表示成无穷多个因子乘积。于是通过联想和类比，欧拉便发现sinx可以分解成下列因子连乘积：

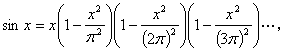
这便是著名的欧拉公式。这个公式利用数学分析方法，可以获得严格的证明，特别有趣的是，如果把上式右端展开，可以看出x³的系数是： ”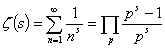

约翰·伯努利听到欧拉的成功消息后极为兴奋地说：“要是我哥哥活着，这将使他最热望的心愿得以满足”。后来这个约翰·伯努利也给出了一个证明，实际上同的欧拉方法一样，都是把多项式根与系数的关系推广到幂级数，严格来讲，这种方法是不能用的，然而，那时的数学家们，似乎对于这样的错误并不介意。

华罗庚在他的《从杨辉三角谈起》小册子的最后，给出了对于全体自然数倒数的平方和的逼近方法，说明全体自然数倒数的平方和会无限的逼近π²/6，但是决不可能就是π²/6。文中通过四步论述了他的逼近方法，其中的第四步可以不断的实施，不断的提高它的准确度。

2、欧拉乘积公式的问题。

1737年，也就是在欧拉给出上述两个欧拉函数值的第二年，他又给出了一个更让大家吃惊的东西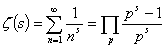： ，这个东西有的书上称它为欧拉乘积公式，有的书上称它为欧拉恒等式。一般来说，数学上的公式必须通过推导演算予以验证，数学上的定理则必须通过十分严密的论述予以证实。让人觉得惊讶的是，欧拉对于它的这个乘积公式，不仅没有推导演算的验证，而且也缺乏十分严密的论述证明，他仅仅只给出了一个如同悖论一般极其简短的说明。

卢昌海写了一本名为《黎曼猜想漫谈》的数学科普著作，王元特意为其写了一篇名为读后感的代序，称赞文章关于数学的阐述是严谨的，数学概念是清晰的。文字流畅，并间夹了一些流传的故事，以增加趣味性与可读性，从这几方面来看，都是一篇很好的雅俗共赏的数学普及文章。卢昌海特意在他的附录A里，介绍了欧拉乘积公式的问题。卢昌海说：欧拉乘积公式的证明十分简单，唯一要注意的就是对无穷级数与无穷乘积，不能随意套用有限求和与有限乘积的性质。然而，无限求和与无限乘积又会具有一些什么样的性质，他们与有限求和及有限乘积又会有些什么样的不同。

笔者认为无限的范围远比有限的范围庞大得多，其中的情况也更为复杂。有限范围里的数，我们可以运用大小予以区分，无限范围里的数，我们不能运用大小予以区分，不知是否可以运用等级的概念予以区分。何华灿出版发行了一本名为《统一无穷理论》的书，似乎他对于无限问题，并没有从数学的角度真正的予以深入研究。在我国的《庄子》一书上，对于无穷问题已经有了明确的记载：“一尺之棰，日取其半，万世不竭”，这个无穷级数的极限为1。上面莱布尼茨在巴黎所证明的那个无穷级数的极限也为1，但是，这是两个完全不同的无穷级数，因为它们逼近极限1的速度是完全不同的，因此 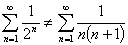。类似的情况可以写出许多。

现在几乎所有的数学书上，全都认为欧拉的证明是毋庸置疑的，因为根据算术基本定理，每一个自然数都具有唯一的素数分解形式。其实，上述欧拉乘积公式的左边，表示的是全体自然数倒数的s次方之和，这是由于自然数是一个公差为1的等差级数，十分规律，可以如此予以表示。然而，右边的全体素数的s次方之积，就不能这样予以表示了。因为素数的分布很不规律，两个素数的间距可以小到只有2，也可以大至无限。

如果全体素数的数量为k个，用p_k表示其中最大的那个素数，那么在p_k和p_k²之间，必定还会存在着许多个大于p_k的素数。因此，欧拉乘积公式右边的全体素数的s次方之积，根本就无法予以如此表示，所以上述欧拉乘积公式根本就不能成立，因为你根本就不能说，全体素数的数量只有多少个这句话。

3、素数定理的问题。

1859年，高斯的学生黎曼，发表了他唯一的一篇数论文章。此篇名为“论给定量以内的素数数目”的文章极其简略，全文总共只有八页，给出了ζ（s）欧拉函数，当s为复数时的情况。最初大家都觉得此文疏漏很大，然而，不久许多人都转变了看法，认为此文可以解决素数定理的误差问题。为了填补黎曼的漏洞，法国科学院于1890年设立了名为“决定一定界内素数个数”的大奖。只有李特尔伍德始终认为，所谓的黎曼猜想完全都是错的。

素数定理：π（x）～x/logx，是近代数学里的一个最最充满疑问的定理。15岁时的高斯曾经猜想过，小于x的素数的个数π（x），或许与x的对数积分Li（x）渐近相等，由于Li（x）～x/logx，所以π（x）～x/logx。其实，高斯的许多数学思想未必都是对的，例如他对于非几何的态度，不仅是错的，而且还涉及到了他的人格问题。对于我这个民间的数学爱好者来说，就已经发现了他的表一个数为二平方和的表数公式根本就是错的。那么他少年时的一个不切实际的胡思乱想，能正确吗？

1896年，阿达马和瓦莱—布桑都是依据了ζ（1+it）≠0，同时分别证明了当N→∞时，π（N）logN/N的极限为1。于是有人称他们是证明了素数定理，给出了素数的分布规律。其实，他们所证明的东西与素数的分布根本就毫无关系，他们只是证明了在无限大的情况下，素数的数量与自然数数量的比几乎为零而已。

英国解析数论大师哈代于1921年，在哥本哈根数学会上，对于素数定理的证明曾说：“断言一个定理肯定不能用某种方法证明是轻率的，……，如果谁给出了素数定理的初等证明，那他就证明了（我们现在关于数论、解析函数论中何谓深刻，何谓肤浅的）见解是错误的，……从而到了该丢掉一些著作来重写理论的时候了。”

然而，就在哈代说出此话的第二十八年，挪威美籍数学家赛尔伯格与匈牙利数学家爱尔特希，双双同时运用初等方法，也分别独立证明了这个素数定理。