1、实际工程所碰到的问题。

“雅都”是苏州第一座顶层为旋转厅的高层建筑，涉及到了圆弧梁的受力分析新课题。由于负责此项工程结构设计的工程师是我的好友，所以对于此项工程的结构设计我也是全力以赴。我在范钦珊和朱祖成合译的前苏联的《材料力学手册》上，总算找到了圆弧构件的静力计算公式，那时只能运用晦涩难懂的虚功原理，通过极其繁琐复杂的运算，支持他顺利完成了此项任务。

以后我又花了几年时间，更加深入地研究了这个课题，发现这个问题竟然十分简单，只要首先将这个假性偏微分方程转化为一个常微分方程，然后经过一种特殊的变换，那么所有的内力变位，就会即刻全部展现在你的面前。1990年，我将这些新发现整理成文，在“现代结构技术交流会”上，与大家作了书面交流，并未引起与会专家们的重视。现在我则觉得其中的一些数学问题，似乎还需要再进一步的搞搞清楚。

结构力学一般研究的是直杆受力分析，它们的内力变位函数只有一个变量x。圆弧梁属于曲杆，尽管其截面具有切向和径向二种内力变位函数，然而，它们的变量还是只有一个，那就是其圆心角θ。因此，我们在研究直杆受力分析时，可以采用直角坐标系予以表示，然而，我们在研究圆弧曲杆受力分析时，还是采用极坐标系予以表示比较方便。如果运用Q表示竖向剪力，M_s表示切向弯矩，M_n表示径向扭矩，那么对于半径为r的微段圆环梁来说，其在竖向均布荷载g作用下的内力的平衡关系为：

Q+△Q=Q+grdθ，M_s+△M_s=M_scosdθ+M_nsindθ-Qrsindθ+gr²（1-cosdθ），M_n+△M_n=Qr（1-cosdθ）-M_ssindθ+M_ncosdθ-gr²（dθ-sindθ）。

由于dθ十分微小，所以可取sindθ=dθ，cosdθ=1，于是即可得到其左向截面的，荷载与内力之间的微分关系为：dQ/dθ=gr，dM_s/dθ=M_n-Qr，dM_n/dθ=-M_s，d²M_n/dθ²=Qr-M_n。从而解得它们的内力函数为：

Q=θgr+C₁，M_n=C₂cosθ+C₃sinθ+θgr²+C₁r，M_s=C₂sinθ-C₃cosθ-gr²。

2、假性偏微分方程的建立。

结构力学里有一些专用符号，择要作一点说明，E—弹性模量，G—剪切模量，EI—抗弯刚度，GJ—抗扭刚度，λ= EI/GJ。对于一个微段圆环梁ABCD来说，如果AB和CD为截平面，AC和BD为边曲面，那么当它竖向位移至A＇B＇C＇D＇位置时，此四个点的位移是各不相同的。不妨假设AA＇=w，由于w是变量n，s的函数，所以B点的竖向位移，可以运用泰勒级数表示为：

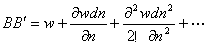
略去一阶以上的微量后得到：

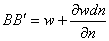
按照同样的道理可知，

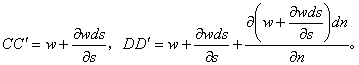
由于AB和CD二平截面的扭转不等，可以算出其相对扭转角为：

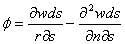
剪应变为：

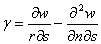
由于AC和BD二边曲面十分微小，可以看作是平面，于是不难得到其切向正应变为：

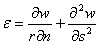
根据虎克定理则有：σ=Eε。按照初等梁理论，梁的截面弯矩为：M_s=∫∫zσdzdr，σ=M_s/I。即有

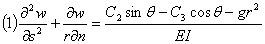
只要按照类似的方法，同样可以得到梁的截面扭矩为；

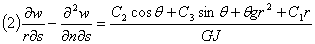
这是一个假性偏微分方程，式（2）对s积分得：

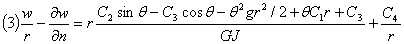
代入式（1）整理后，即得二阶常微分方程：

（4）w＇＇+w =（C₂sinθ-C₃cosθ-gr²）r²/EI +[C₂sinθ+C₃（1-cosθ）+θ²gr²/2+θC₁r]r²/GJ+C₄

式中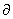w＇＇= ²w/ 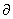θ²，dθ=ds/r。等号右边的第三项C₄是与边界给定变位部分有关的常数。第一项其小括号里的算式，是弯矩函数的表达式。第二项中括号里的算式，是扭矩函数的表达式。

3、二种特殊的变换。

由于内力是变量θ的函数，所以还可以将上述二阶常微分方程表示为：

ƒ（θ）=（1/EI+1/GJ）r²C₂sinθ－（1/EI+1/GJ）r²C₃cosθ+gr⁴θ²/2GJ+C₁r³θ¹/GJ+（C₃r²/GJ－gr⁴/EI）θ⁰

等号右边的最后一项，是与边界给定外力（由内力转化）部分有关的常数，为了区别于C₄常数，所以将其乘以θ的零次方。由此得到二阶常微分方程（4）的一般型为：

（5）w''+w=Asinθ+Bcosθ+Cθ²+Dθ¹+Eθ⁰+F

式中的A，B，C，D，E，F为常数，不妨假设其特解为；

y₀=H（θcosθ-sinθ）+Jθsinθ+K（θ²+2cosθ-2）+L（θ-sinθ）+M（1-cosθ）+N

为了求取特解y₀中的待定系数H，J，K，L，M，N，将次求导如下：

y₀＇=-Hθsinθ+J（sinθ+θcosθ）+K（2θ-2sinθ）+L（1-cosθ）+Msinθ

y₀''=-H（sinθ+θcosθ）+J（2cosθ-θsinθ）+K（2-2cosθ）+Lsinθ+Mcosθ

由

y₀''+y₀=-2Hsinθ+2Jcosθ+Kθ²+Lθ+Mθ⁰+N

得：

H=-A/2，J= B/2，K= C，L= D，M= E，N=F。

由此即可得到上述二阶常微分方程（4）的解为：

（6）w=C₄+C₅cosθ+C₆sinθ+（C₂sinθ-C₃cosθ-gr²）[sin²θ+λ（1-cosθ）²]r²/2EI－（C₂cosθ+C₃sinθ+θgr²+C₁r）[（θ-sinθcosθ）+λ（θ+sinθcosθ-2sinθ）]r²/2EI ＋（θgr²+C₁r）[（θ-sinθcosθ）+λ（3θ+sinθcosθ-4sinθ）]r²/2EI －gr²[（1-cosθ）²+λ（θ-sinθ）²]r²/2EI。

这是圆弧曲梁在竖向均布荷载g作用下的挠度曲线函数，等号右边的七项，全都有着十分明确的力学意义。前面三项表示边界给定变位部分，即支承处截面位移，弯转，扭转所引起的挠度分量，可以运用几何方法予以复核。后面四项表示跨间荷载及截面内力所引起的挠度分量，只能运用力学方法予以复核。

其实，对于式（6）来说，我们也可以通过拉氏变换得到。如果将ƒ（θ）的拉氏变换表示为ζ{ƒ（θ）}，那么，由于初始条件w₀=0，w＇₀=0，所以式（5）等号左边的拉氏变换为：ζ{w＇＇}+ζ{w}= s²ζ{w}-sζ{w₀}-ζ{w₀＇}+ζ{w}=（s²+1）ζ{w}。等号右边的拉氏变换为：ζ{Asinθ+Bcosθ+Cθ²+Dθ¹+Eθ⁰}= A/（s²+1）+Bs/（s²+1）+2C/s³+D/s²+E/s。得到

ζ{w}= A/（s²+1）²+Bs/（s²+1）²+2C/s³（s²+1）+D/s²（s²+1）+E/s（s²+1）

= A[1/（s²+1）-（s²-1）/（s²+1）²]/2+Bs/（s²+1）²+2C[1/s³+s/（s²+1）+1/s] +D[1/s²-1/（s²+1）]+ E[1/s-s/（s²+1）]

由此同样可以得到式（6）之挠度曲线函数。式（6）之挠度曲线函数代入式（3），即可得到其扭转曲线函数，扭转曲线函数的微分为扭矩曲线函数。挠度曲线函数的微分为弯转曲线函数，弯转曲线函数的微分为弯矩曲线函数，弯矩曲线函数的微分为剪力曲线函数。只要支座条件一旦确定，即可通过一个六阶刚度矩阵的求逆，具体得到这三个内力和三个变位。其实，这是笔者的一个尚未完全考虑成熟的问题，笔者之所以急于要将这个问题提出来，是因为这是一个十分重要的实际应用问题，希望能引起专家们的关注，既要更深入的进行研究，更要设法予以开发利用。