1、《孙子算经》的作者。

根据《隋书·经籍志》的著录，那时的《孙子算经》只有上下二卷。随后的《张邱建算经序》有云：“其夏侯阳之‘方厄’，孙子之‘荡杯’”，而传本《夏侯阳算经序》又云：“五曹，孙子述作滋多”。由此可见，《孙子算经》是隋代以前的数学专著，并且比《张邱建算经》和《夏侯阳算经》更早面世。因此，清初的朱彝尊在其《孙子算经跋》里，认为《孙子算经》的作者，应该就是《孙子兵法》的作者孙武。

其实，我们只要根据《孙子算经》的主要内容，即可断定此书必定也是孙武的著作。“筹算”是《孙子算经》里的一项重要内容，算筹是我国上古时代的唯一的运算工具，那时能够运用这种运算工具的人不多，精通“筹算”方法的人更少。《列子》“说符”篇记载说：“卫人有善数者，临死，以诀喻其子。”由此可见，掌握这种运筹算法的人，直到临死才肯传给其子。然而，孙武在他的《孙子算经》里，却将所有的“筹算”方法全部予以公开，由此推动了我国古代数学的飞跃发展。

我们现在所看到的《孙子算经》则有上中下三卷，其下卷载有“户输绵二斤八两”之户调法，还编有“棋局十九道”之题。由于户调制乃晋武帝时开始实行沿用至唐，三国时吴国邯郸淳的《艺经》尚称围棋十七道，由此可见，流传至今的《孙子算经》，在隋代以后，就有几个多事之人对其作过一些增补，充实了一些新的内容。

乾隆年间的戴震在参与编撰《四库全书》时，仅仅根据《孙子算经》上载有“今有长安洛阳相去九百里”，“今有佛书凡二十九章”，就断定《孙子算经》决非孙武所著，因为“长安”是汉初才有的地名；而“佛书”一词则产生于东汉。这就是乾嘉学派所掀起的那股“吹毛求疵”的歪风，这股歪风硬是将《周髀算经》从西周刮到了西汉，将《九章算术》从东周刮到了东汉，更是将战国初期的《孙子算经》，一直刮到了更晚的南北朝时期。

其实，戴震对于我们的中国数学，也仅仅只是一个一知半解的门外汉，他在《四库全书提要》里，评价秦九韶的大衍求一术时说：“其法虽不尽精密，而大衍数中所载立天元一法，为郭守敬、李冶所本。欧罗巴之借根方，至为巧妙，亦从此出也。”混淆了求一术与天元术中的“天元一”的区别，竟然闹出了如此笑话。

如果按照戴震的观点，只要有人对于孙武的《孙子算经》作过增补，增补过的《孙子算经》的作者就不再是孙武了。那么，传至今天的《几何原本》，就更不是公元前三世纪欧几里得的著作了。因为史载埃及女数学家希帕蒂娅，曾经协助其父完成了对于《几何原本》的第一次修订。以后的《几何原本》又长期流失在外，长达上千年之久。今天我们所看到的《几何原本》，实际上是伊斯兰大学的一本教科书，不知经过了多少人的修改及增补。现在有些人不是热中于什么都要与国际接轨吗？那么在判断一部古籍的成书年代问题上，为什么却不与国际接轨了呢？怎么可以另搞一套标准呢？

2、“物不知数”问题。

“物不知数”问题是《孙子算经》下卷里的第二十六题，此题为：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”答曰：“二十三”。术曰：“三三数之剩二，置一百四十；五五数之剩三，置六十三；七七数之剩二，置三十。并之，得二百三十三。以二百一十减之，即得。凡三三数之剩一，则置七十；五五数之剩一，则置二十一；七七数之剩一，则置十五。一百六以上，以一百五减之，即得。”

术文的前半段给出了本题的解法为：N=70×2＋21×3＋15×2－105=23。而术文的后半段，则给出了这类一次同余式组：N≡R₁（mod 3）≡R₂（mod 5）≡R₃（mod 7）的一般解法为：N=70R₁＋21R₂＋15R₃－105P（P为正整数），这是因为1≡70（mod 3）≡21（mod 5）≡15（mod 7）。由此可见，现代数学里的同余式组的问题，对于中国数学来说，却是一个十分古老的问题。由于这个“物不知数”问题可以直接称为孙子问题，所以上述术文则可以称为“孙子算法”。这个“孙子算法”，北宋的周密称之为“鬼谷算”，“隔墙算”；南宋的杨辉称之为“秦王暗点兵”，“剪管术”；明代的程大位称之为“物不知总”，“韩信点兵”。

或许有人要问，这道“物不知数”问题，到底是孙武的原作？还是后来多事之人的伪作？这个问题很难予以解答。笔者认为只有曾经当过吴国将军的孙武，才有可能提出这个与行军布阵密切相关的数学问题。我国春秋战国时期的道家著名人物，他们往往既是一个军事家，同时也是一个数学家，例如“田忌赛马”的故事。其实，孙武的《孙子兵法》，实际上也是一部运筹学著作。

根据我国的商代已经在使用完善的六十干支记日法，可知我国早在商代之前已经掌握了，运用“更相减损术”求取最大公约数和最小公倍数的方法，说明那时的孙武完全具备了提出“物不知数”问题的数学背景。然而，我国古代历法的编制，从汉初开始出现了，必须首先根据“孙子算法”推算出“上元积年”的怪事，从而将我国对于合数环的研究，引上了一条歪路。

其实，对于一个合数环H_ef来说，只要e与f互素，那么这个合数环里的ef个元素，与由H_e分环和H_f分环所构成的ef个同余式组之间，完全是一一等同的。H_ef合数环里的种种特性规律，原本都是H_e分环和H_f分环的特性规律，通过这ef个同余式组传递过来的。反过来说，只要H_ef合数环具有某种特性规律，那么它的各个分环也必定会具有这些特性规律，这是我们今天需要认真研究的问题，H_ef合数环的内部结构则是又一重要内容。

3、“孙子定理”的问题。

《孙子算经》里的“孙子算法”，是解开各个模数全都两两互素，并且其模数的素因子的方次也全都低于2的同余式组的方法，由此可见，“孙子算法”对于模数的限制是极其严格的。然而，若是对于同余式组的模数如果不作上述种种限制，让它们可以不必全都两两互素，并且其模数的素因子的方次也不必全都低于2的同余式组的解法，则称为完整的“孙子算法”，或干脆称之为“孙子定理”。

笔者认为祖冲之在他的“大明历”里，已经将孙武的“孙子算法”发展成了一个完整的“孙子定理”。祖冲之是根据以下八个同余式组，来推算他的“大明历”里的“上元积年”的。显然，在这八个同余式组里，前七个同余式的模数具有最大公约数2，后二个同余式的模数具有最大公约数3。

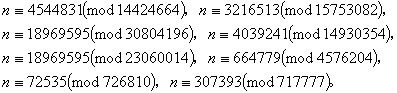
由此解得上元积日为n=18969595日，换算成上元积月和积年则为：642371月和51937年。我国古代的历法认为，年始于冬至，月始于朔旦，日始于夜半，甲子日夜半朔旦冬至，……，以此作为历法中节气，朔望，日月食和五星的共同起身点，是为上元。从上元到治历的岁数，称为“上元积年”。史载在“大明历”问题上，祖冲之与权臣戴法兴之间曾发生过一场论战，看来真理应该是在戴法兴一边，因为那时首先推算“上元积年”的荒谬浪潮已在消退。

如果只是从数学的角度上去看，祖冲之的“大明历”确实发展了孙武的“孙子算法”。然而，若是从历法的角度来看，祖冲之的“大明历”对于“上元积年”的推算，可谓搞得变本加利的荒谬。其他人对于“上元积年”的推算，只是除了日月之外再加上一个木星而已，然而祖冲之却硬是要将金木水火土也一齐都加了进去。

南宋的秦九韶不仅将这个完整的“孙子算法”从历法之中分离了出来，而且还给出了迅速计算乘法逆元的“大衍求一术”。秦九韶对这个“大衍求一术”十分得意，放在了他的《数书九章》的首要位置。这个完整的“孙子算法”于1852年，由英国传教士伟烈亚力传到欧洲，被称为“中国剩余定理”。