如果我们的宇宙是一个多维空间，我们怎么保持象GPS那样定位，参见科学智慧火花物理学栏目，

空间的维度：http://idea.cas.cn/viewdoc.action?docid=62446

定位是可能的，还是有章可循，居然用得上哥德巴赫猜想、费马大定理和黎曼猜想，以及欧拉公式，与P=NP问题有关。

利用素数基本性质，借助霍奇猜想的方法，可以把哥德巴赫猜想用图像表示。这种图像就是费马大定理的数学模型，计算这个模型时候就要用黎曼猜想的方法，这个模型也是弦理论的模型。这样数论与几何联系起来，它是【朗兰兹纲领】的一部分，并且与物理学最重要的问题融为一体。

几何构造比代数少多了，而且远比代数构造难度大太多。这个几何构造需要一系列重大数论构造来联合表示。本文的几何拓扑构造就是在哥德巴赫猜想费马大定理黎曼猜想的框架中，理论物理最终会变成几何和数论的一部分。

一，数论的最高境界就是应用于实际并且把许许多多的问题融合在一起

（一），从四色定理开始

法兰西斯古德里于1831年生于伦敦，在1852年提出的猜想，只需要四种颜色为地图着色。这是因为他发现在平面上或者球面上，只能有4个区域两两相连，英国数学家德摩根证明了平面上不存在5个区域两两相连。

1974年德国的林格和美国的杨斯证明了在曲面上染色定理，例如，在一个汽车轮胎形状的环面需要7种颜色，因为可以构造7个两两相连的区域，6种颜色肯定不够的；在有两个洞的双环面需要8种颜色，因为可以构造8个两两相连的区域，7种颜色肯定不够的；....。(具体图像参见百度百科“n色定理”）

（二），岐管

数学家证明了可以构造无穷多个两两相连的区域，这样的区域就是岐管。

如果你不能理解，让我慢慢道来：现在有两根管子，一个记为1，一个记为2，它们代表两个区域。

我们假定所有的管子都是可以随意拉伸和弯曲的。

把两根管子端端相连，就是一个汽车轮胎一样的环，它有两个区域，我们再用一根直管子记为3，安在这个环的中间，一头连着区域1，一头连着区域2，现在它是有两个洞的双环了，有三个区域两两相连（霍奇猜想，参见智慧火花数学栏目【数学最重要的问题与物理学最重要的问题可以结合在一起吗】）。

现在我们用一个“丁”字型的三叉管，记为区域4，三个端口分别与区域1，区域2，区域3相连。于是现在有4个区域两两相连；

我们再用一根四叉管记为区域5。它4个端口分别与区域1,2,3,4相连，现在有5个区域两两相连。

这个步骤可以无限制进行下去，用五叉管，六叉管，...，n叉管。构造无穷多个区域，它们都是两两相连的。

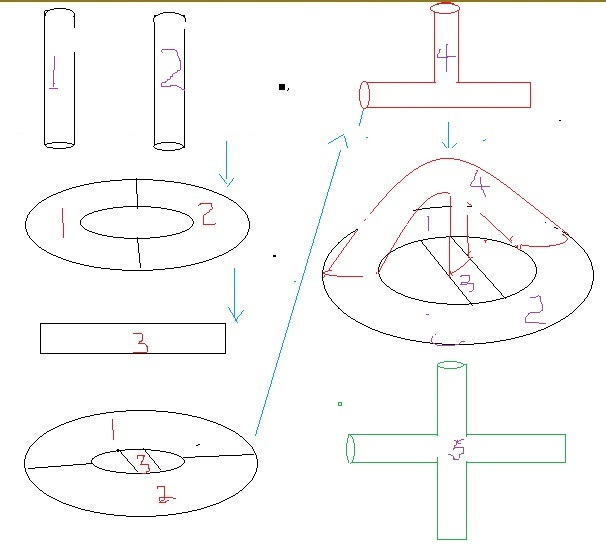
<p ">数学家和物理学家把这个叫做岐管。岐管是一种不规则的管道，可以有无穷多个维度（参见智慧火花物理学栏目【空间的维度】）这个歧管可以等价转换成为“货郎担问题”，与P=NP问题相联系。

二，与数论联系

在数论中，最重要的元素就是素数，欧几里得证明了有无穷多个素数，并且它们有一个特点就是两两互素。

我们把无穷多个两两互素的素数与无穷多个两两相连区域一一对应。

就是说用这个方法把数论与图论联系起来，这个方法的意图叫做朗兰兹纲领。

区域1，代表第一个素数2；第二个区域代表第二个素数3；第三个区域代表素数；...，第n个区域代表第n个素数。

我们把这个岐管倒过来，就像一个网子，篮球网子。篮球网子是把篮球往里面投。

公元前300年古希腊有一个数学家叫做埃拉特斯特尼，他把这个网子当成筛子，把自然数往里面扔，他说凡是合数通过筛子以后就会从网子里面筛掉，留下的是素数，这个就是著名的埃拉特斯特尼筛法，筛法可以用公式表达（参见百度词条【素数普遍公式】）。

二，与哥德巴赫猜想联系一起了

我们上面这个岐管筛子是把偶数往里面扔，哥德巴赫说，大于4的偶数一个也不会漏出筛子，除了6=3+3以外，其他偶数都是可以在不同的素数区域被拦截。例如偶数8会在区域2也就是素数3和素数5（第三个区域）被拦截；偶数10会在素数3和素数7的两个区域之间被拦截；...。总之，无穷多个偶数都逃不脱这个网子，没有一个偶数可以漏到外面去。

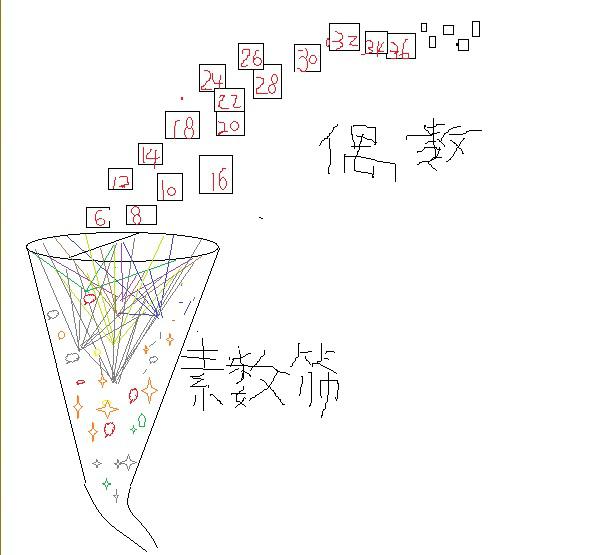
看到没有？数论与图论已经融合一起了

三，与费马大定理联系一起

这个还不算神奇，这个岐管的内部空间我们记为X，外部空间记为Y，它有很多洞,可以有无穷多个洞，可以有无穷多个空间维度n，宇宙内外整体记为1，就是说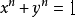，这个叫做费马曲线，它是由费马大定理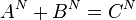同时除以C^N得到的。

费马大定理与哥德巴赫猜想联系起来了。

四，这个岐管就是多维空间

物理学家认为，宇宙是10维空间或者11维空间，或者26维空间等5个版本。还有物理学家认为有无穷多个维度的空间。他们管这个理论叫做玄理论或者M理论，是把广义相对论与量子理论结合一起的终极理论，霍金说是最后的理论（参见智慧火花物理学栏目【空间的维度】）。

五，与黎曼猜想联系起来

数学家考虑的是怎样计算这个岐管上的区域或者计算区域上面的一个点（就是计算我们的宇宙定位系统）。如果岐管上某一个区域n，在n上的一个点是1/n，因为这个岐管有无穷多个维度，或者很多维度，我们要定位这个点，就要考虑它的管壁-----实部，还有考虑它的内外空间位置-----虚部。

所以，这个点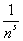，S=α+βi。

i是虚数，α表示实部是1/2，因为这个多维宇宙等于1，岐管属于实部，管壁介入X与Y之间，实部上的点当然是1/2。这个正是黎曼函数黎曼猜想：

。

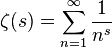黎曼猜想说全部零点都在实部的1/2的临界带上。在物理学中，真空是能量的“零点”。我们如果在岐管壁上画出一条线，这根线段就用到黎曼猜想的公式计算。

黎曼猜想与费马大定理联系起来了（参见智慧火花物理学栏目【两个数论黑洞合并以后产生的引力波】）。

六，与欧拉公式联系起来

与欧拉公式联系起来，虚部怎么计算呢？岐管内部看成一个圆管，在岐管上的一个点为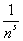，做一个截面，就是一个圆。大家知道欧拉公式吗？

 。

以e^0 =1开始，以相对速度π，走了i时间(参见百科百科“虚时间”)，再加1，回到原点。

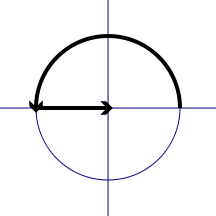
包含了时间(时间有虚的涵义)和空间。

虚时间是为了对应时间起点（大爆炸）而定义的一个概念。在虚时间这个概念体系里，在比三维更高的维度空间，时间并不是一条直线，而是一个闭合的圆，没有起始也没有终结，

如果走过头，假如超过了π，走到了3.1416，让我们看一下会发生什么情况：

.....，式（1）

因为圆周率：

π=3.141592653.... ，.......式（2）

于是公式（1）为：

..... ,式（3）

π=3.141592653.... = 3.1416 — 0.000007346...。式（4）

公式（3）变为：

，式（5）

我们知道，同底数相除，指数相减  ，反过来也一样，即同底数指数相减，就是两个数相除

，式（6）
。式（7）

（7）太荒唐了！但是却是一个现实。

当大于π时，就是时间走过头了，落入第三象限。欧拉公式是将指数函数e^πi解析延拓到整个复平面上。虚时间就是——（7）式物理学中出现这种情况：

不同时代的人在一个特殊的空间相会，例如今天的人（e^3.1416i）与3000年前的人-e^0.000007346i

相遇（或者今天的人与未来的人相遇），我们会感觉到什么？

（7）式可以刻画量子纠缠——在同一时间两个正负不同的光量子对应。

我们的宇宙是由数学最经典的问题和物理学最经典的问题组成的。

我们生活在费马大定理的宇宙中，出门旅行计算路程需要黎曼猜想，在欧拉公式的参与下，穿过哥德巴赫猜想的虫洞。一具复杂的岐管，包含了一个超级几何拓扑构造，需要一系列重大数论问题联合表示。即使不是与物理学联系，也是非常重要的。