至今，光仍是人们宏观上最熟悉而微观上又最迷惑的东西。1666年，英国物理学家Newton提出了光的弹性微粒说（Corpuscular theory）,他的粒子说流行了近一个半世纪。虽然芬兰物理学家Huygens于1679年就提出了光的波动说，但其认为光是在特殊介质“以太”（ether）中传播的弹性波，因为科学界否认了以太的存在而其波动说一直没有得到公认。直到1801年，英国物理学家Young观察到了被后人称为杨氏双缝衍射的现象之后，波动说才渐渐为人们所接受。1861到1862年，英国物理学家Maxwell提出了光的电磁波学说，波动说终于成了主流。不过，到了19世纪末与20世纪初，发现的光电效应和黑体辐射使光的波动说受到了严重挑战。至此，光的每种学说都曾受到过种种的质疑。1905年，聪明的爱因斯坦仅以最笼统简捷的公式E=hv，提出了光量子学说，结束了长期以来关于光的波、粒之争，并把人们对光子细节的迷惑与不解留给了读者和后人。爱因斯坦的光量子学说没有遭到太多的质疑，但至今人们尚未完全知道光究竟是什么，光的某些属性也还让人捉摸不定。

纵观光学史的曲折性与光的复杂性，旧的光学现象，如光的衍射和相干等疑惑依旧存在，新的有关光子纠缠、量子通信密钥、奇异光子行为等的难解之迷又不断出现。由于历史的教训，今天我们在重新审视光的本质时就必须要特别小心。我们必须总观丰富多彩的光学全部实验现象，把所有有关光的事情联系在一起，然后找出蛛丝马迹，将已有充分细节而无法证实的那些项罗列在一起，作为数学上一道证明题的已经条件，然后进行推理与求证，争取认清光子的本来面目。

在真空中传播的光子究竟什么样，依据上述历史，人们最先想像成的是弹性的乒乓球，更可想像成水中微风吹拂下的波纹。各大学物理及光学教材的各种图例中，把光子画成带箭头的波纹线；也有人认为光子是一个环，维基百科在光子角动量词条下，更是把光子画成了螺旋，还有的将光子画成螺旋状的面包状或大麻花状，在大学的无机化学及分析化学教材中也常把光子描述成坡印亭矢量。本作者在《光子不是一个环，也不是一个螺旋》一文^[1]中，通过多种光学定律及实验现象，对上述人们关于光子形态的猜测和描述进行了分析，并认为真空中传播的单光子的形态整体上类似于一个艾里波列，分段及内部结构可用坡印亭矢量来描述。

我们考虑光源原子或分子中的电子对光子的分娩过程，实际上是电子从高能级跃迁到低能级的过程。这不是一个瞬时过程，对于普通光源，大学物理教材中认为耗时通常小于10^-8秒^[2]。根据量子力学知识，原子或分子中电子的运动，虽然不像太阳系中的行星运动，但根据波函数与电子云概念，电子还是会按波动形式绕核运动的。显然，电子对光子的分娩不是绕核一周就能完成的。如果这个作用时间在10^-8~10^-10秒之间，我们根据氢原子的玻尔半径0.053nm和1/137光速的电子经典绕核运动速度来分析，氢原子每辐射一个光子，电子需要绕核运动的周次数大致为：

[（3.0×10⁸m/s）/137] × （10^-8~10^-10s）/（2π× 0.053× 10^-9m）=6.6×（10⁷~10⁵）（周次）

计算表明，氢原子完成一次辐射花费的时间t若为10^-8~10^-10秒，那么它分娩出一个光子的过程，就要绕核转过大约十万到千万个周次。电子绕核的旋转频率与辐射光子的频率大致相当（在同一数量级），但由于电子与光子的速度相差137倍，因此两者的波长却大致相差两个数量级。综合分析，通常电子从一个高的能级跃迁到低能级时要经过几十万到几千万个绕核周次才能发射出一个光子波列，光子的单色性越好，电子需要绕转的周次数越大。总之，通常的一个光子应该是一个波列，而不是电子绕核一周就能辐射出的一个环。当然，对于光孤子的情况可能比较特殊，可能对应于电子的单个绕核周次。

在原子或分子中的电子处于束缚态，其能量为负值，能级越高，其能量的绝对值越小。电子在高能级时通常绕核半径比较大，在低能级时绕核半径比较小。因此相对应的一个辐射波列的列头的波长应该较长，列尾的波长应该更短些。波列中相邻的两个波的长度之差就应该是谱线的线宽Δλ。Δλ所对应的能量应该是？的整数倍，而且最小不能低于？。单色性最理想的激光的线宽Δλ所对应的能量就应该是一个？，这是由量子化决定的。任何单色性最好的激光的线宽也不能为零，如果为零，谱线也就不会被观察到了。

波列的长度L=c × t。例如，钠光灯发射的光波的波列长度约为1.4500000000000002px；低气压镉灯发光的波列长度约为1000px；低气压氪灯发光的波列长度约为1750px；单色性比较好的氦-氖激光发射器的激光的波列长度约为10⁵cm（上千米长）。光源的单色性越好，谱线宽度越窄，则光子波列越长。通常波列的长度L与其中心波长（center wavelength）λ的平方成正比，与谱线宽度Δλ成反比^[2]，即 

L=λ²/Δλ.               （1）

（1）       式可改写为

（L/λ）Δλ = λ          （2）

（2）       式中的（L/λ）表示一个光子波列所含有的波次数。

通常一个光子波列的列头波长稍长，列尾的波长稍短，这刚好是艾里函数(Airy function)所描述的情况。

数学上的艾里函数（y = Ai[x]）是二阶微分方程y〞– xy = 0^[3]的解。1979年，Berry和Balazs^[4]在量子力学范畴内得到了类似于薛定谔方程的一种无衍射波包的艾里函数解。但艾里函数与薛定谔方程的解在空间和时间变量上的作用刚好相反，因此经常有人称其为非力场情况下薛定谔方程的一个特解。薛定谔方程只是中心势场中空间坐标的偏微分方程，其解是不含时间的，也可以说是对时间取了平均的一种几率描述。而艾里函数则是一种隋时间变化的沿空间某个方向具有某种延续的动态表述。由艾里函数描述的光波，也称艾里脉冲(Airy pulses)、艾里束(Airy beam)或艾里波包(Airy wave packet)。

由于艾里函数带有无限长的尾巴和无限大的能量，是一个很难与实际应用相联系的数学函数，多年来并没有受到人们的重视。直到2007年，Siviloglou和Christodoulides^[5]采用“截尾或截趾”法处理艾里函数，并从实验上得到了含有有限能量和有限长度的截趾艾里脉冲(truncated Airy pulse)。由于这种截趾的艾里脉冲具有几乎无衍射且具有自愈性的特性，引发了近年来科学界对艾里光束的研究热潮。

本文认为，不但在奇异光子与量子光学领域，艾里光子具有不凡的表现，而且截趾的艾里波列更具有描述普通光子形态的普遍性。只有一个波的特短波列就应该是光孤子，光孤子也是近年来研究的热点^[6]。

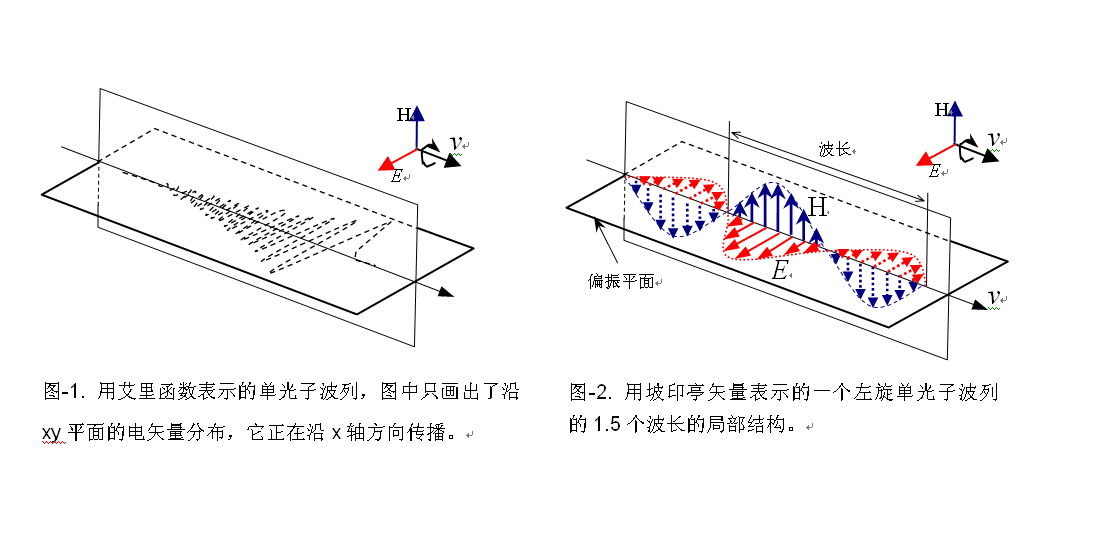
如图-1所示，一个艾里波列实际上就是一个真空中传播的单光子的形态。如图-2所示，光子波列的内部结构可用坡印亭矢量来说明，但光子的整体情况不同于坡印亭矢量。因为坡印亭矢量所表示的长波列中的所有波的振幅都是相等的，相邻的两个波之间没有差别，这样的波列没有光谱线的线宽，是看不见的。也就是说Δλ =0的波列不携带能量，是不存在的。

本作者发现，艾里波列模型能够很好地阐明有史以来所发现的所有关于光的本性的疑惑，包括普通光的相干性及奇异光子的量子纠缠等。相关内容将专笔另外讨论。

参考文献

1.王孝恩，光子不是一个环，也不是一个螺旋，中科院科学智慧火花，20171118.

2.莫文玲,盛嘉茂. 简明大学物理，上册，北京，北京大学出版社，2005年.

3. M. Abramowitz, I. A. Stegun, Handbook of mathematical functions, Nat. Bureau of Standards, (1964).

4. M. V. Berry and N. L. Balazs, Am. J. Phys., 47, 264 (1979)

5.G. A. Siviloglou, and D. N. Christodoulides, Optics, Letters, 32, 979 (2007).

6.张露, 张健, 肖燕. 啁啾艾里脉冲和孤子在非均匀光纤中的传输.中国激光，2017年第44卷第9期 pp.0906005.