提要新的生成函数为节水灌溉提供方案：有限的水量如何灌溉最大面积的农田。把这个问题转换成，铺设一个水管网，有限水量在管网中的流过面积越大，水管网对应灌溉的农田面积也就越大。

引言

我国田间灌溉大多都属于传统的地面灌溉方式，喷灌、微灌及管道输水灌溉等先进节水灌溉技术覆盖率不足10%。⁽¹⁾如何提高节水灌溉效率，扩大农田灌溉面积，生成函数提供了一种理论方法：分组的出水口在水管网上如何分布使可灌溉的面积最大。

一 水管网

农田管网一般采用树状管网，并以单个给水栓进行布置，水管网有n个小孔，一定水量从给水栓注入管网，又从小孔流出到管网之外。水在管网中流过的面积与管网小孔出水量和分组的小孔在管网上的分布有关。 农田灌溉中水的流域，可以用墨汁和水杯的关系来比喻。一滴墨汁落在一杯水，水会变色，一杯水就是墨汁的流域。这些自然现象都可以用生成函数来表示。

农田滴灌（图片来自网络）

1，分层水管网。设水道按照一分为二的方式构型，即以一分二，二分四，四分八，…，管网以n至2n的方式组网，因此，虽然铺设的管网是多形状的，但管网构型是分层的。每一层管网的面积之和，等于最初的注入水量的面积(静态面积)。这意味着随着分层数的增加，水网分布越来越密。即有如下图示

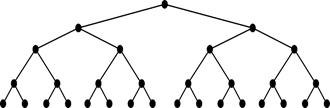
网络树

单水源(用给水栓表示)的管网图示。图中的小点代表水管分支接口，每一个分枝接口上有出水孔，分枝上一个方向让水进入下一个枝管，另一个方向让水从小孔流出管网。在其他因不变的条件下，下面考虑几种操作放水情况。

2， 让水在管网中循环流动，如果没有漏水的话，在相同时间内，水流过的水管的面积为

A＝nA₀(n＝1，2，3，…)

式中A表示灌溉面积(hm²)，A₀为从给水栓注入水的静态面积，A为水在网中流过的总面积，即是动态面积。n为水流的循环次数。在水量一定时，水流过的总面积(动态面积)等于最初面积与循环次数的乘积。

3， 让水以一定比例从小孔流出管网，在水网中继续流动的水所占面积为A₁，流出水管网以外的水量所占面积为A₂，则在管网中的面积等于

A＝A₁＋A₂

由于小孔流水是受控制调节的，每次内流的水占比为x，从水阀外流占比为（1－x），即

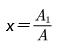
将上式整理有

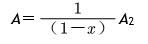
在上式中，1＋x＋x²＋x³＋x⁴＋x⁵＋……＝1／（1－x）为几何级数公式，这些幂级数称为生成函数。由于水管网中的水最终会流尽，并且流出水管网中的水等于(忽略其它损失)最初注入水网的水，设从外部注入的水量的静态面积为A₀，因此A₂＝A₀，带入上式有

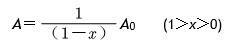
上式表示，当入水量一定时，几何级数1/(1-x)越大，流域面积就越大。1-x越大，x越小，表示小孔出水少，或者小孔喷速越低，剩余的水多，对应的可以继续灌溉的面积就越大。反之，1-x越小，表示x越大，小孔出水量大，或者小孔喷速越高，能够继续灌溉的面积越小。

如果每个水管网上的小孔出水量一样，则出水量面积为各小孔数乘以小孔出水比(1－x)，还要乘以静态水量面积，即

A＝(1－x)nA₀(1＞x＞0)

特殊地，若(1－x)＝x²，则x≈0.618，这是黄金分割数，表示水管网逐级都保持0.618的水量，则有

A≈0.328nA₀

虽然在短程和出水口较少的低压输水工程中存在以上情况，但是，对于等间距、等流量分流的多孔管网，流量会沿流程逐段递减。因此生成函数适用于水量逐段递减管网设计。

4，经过小孔出的水，若只按水量的（1－x）流出，余下的x水量继续循环至下一个喷口，仍然又以（1-x）比例流出管外，余下的x水量继续循环，这个过程循环下去，新增流域面积为

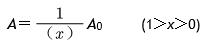
水管网的总流域面积为两流域面积相加，即

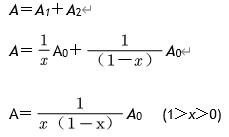
当且仅当

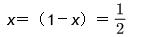
时，x(1－x)有最大值⁽²⁾，则1/x(1－x)的最小值为1/0.25＝4，即在管网环流和外流水量相等时，静态面积4倍是最小的动态面积。

对于生成函数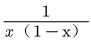，列出矩阵图如下：

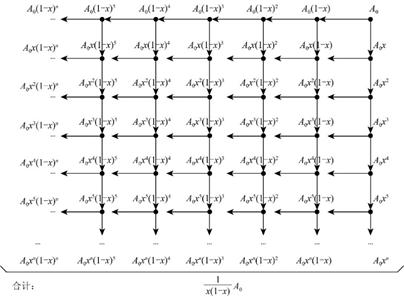
生成函数排列图

若把支管道延长，可以做成正方型、长方型等各种排列。也可以采用多源汇流方式，两头有给水栓，形成一个正方形网。

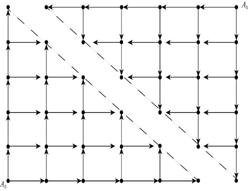
双水源汇流管网示意图

图中A₀表示给水栓的位置，管网上分布出水孔，箭头表示水流方向。

二 变量随机分布的生成函数

1，介绍新函数。上面初步介绍了水管网与生成函数的关系，本文重点是：若小孔出水量一定时，小孔如何分布使管网的可灌溉的农田面积最大。因此，需要介绍一个新的生成函数⁽³⁾即

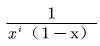
笔者在《经济学新论：乘数、统计熵与国民收入》一书中，证明了这个函数，这里不赘述了，在经济学中的函数称为储蓄随机分布条件下的收入乘数。

2，出水口随机分布。如果出水口在水管网上按照最大概率原则分布，就可以把上式应用于农田灌溉，则有

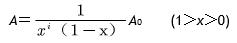
式中的i表示出水量不同的i组小孔，小孔按组在水管网上随机分布。当i＝0，表示小孔不分组，函数是1/(1－x)形式。当i＝1时，有了一组不同出水量的小孔，函数是1／x(1－x)的形式。i值越大，小孔分组数越多，生成函数值越大，管网面积越大。i值越小，生成函数值越小，管网流域越小。i趋大表示管网上出水孔分组趋密，相对应的孔径等比趋小。管网上分组的出水口随机分布会使有限水量的灌溉面积趋于最大化。

出水口随机分布是一种均匀分布。小孔按组随机分布可以使水管网的出水量实现各段均匀出水。前段管网随机分布一些小出水量的小孔，后段管网随机分布一些大出水量的小孔，实现水管网整体均匀出水。避免前段水管出水量大，后段水管出水量小的情况，使农田得到均匀灌溉。

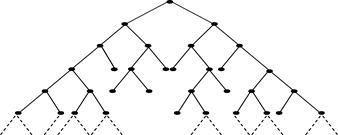
随机两项分枝网络

上图称为马尔可夫链⁽⁴⁾，表示逐渐消失的随机分布的网络流域。

出水孔在管网中随机分布的图形，需要综合考虑地形和农作物的耕种环境，并且以给水栓位置为中心做规划设计，以下是一个方格图的随机排列：

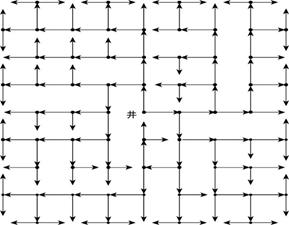
出水口随机分布的方格管网

在上图中，给水口在网络中间，井字代表水源，表示从机井取水。箭头表示输水方向，每个节点按一分为二连接，随着管网分岔延伸，出水口按等比关系分组，出水孔随机分布在方格网络上。方格图没有边界，理论上可以无限细分，方格图的表达函数是/xⁱ（1－x），因此它是一个出水量均匀分布的管网。

三 组合的生成函数

一般而言，生成函数还有多种计算方式，并且完全可以运用于现有的微灌网络设计，例如下面是一个典型的树状管网设计，仍然可以用生成函数的方法来设计管网，用于节水型的农田灌溉。

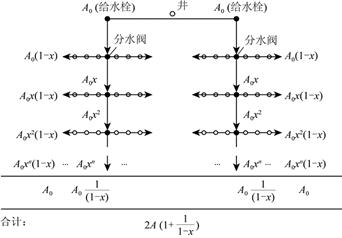
树状管网

图中的井指机井。机井抽水向两边给水栓，管网的水通过分水阀逐级分流出管网。动态的流域面积为静态流域面积的2[1＋1／(1－x)]倍。如果地形由高至低，可以选择一个机井连一个管网，在平原区布网可以迭择双向供水⁽⁵⁾，以便土地水量供给相对均衡。管网设计还可以把确定性与随机性小孔出水结合起来，达到田间复杂布局的要求，用函数相加来设计管网，即

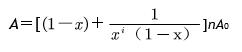
在以上公式中，即有传统的灌溉布局关系式，又有生成函数，还包括随机分布的管网函数。

小结

综上所述，水管网上的出水口随机分布会使有限水量的灌溉面积趋于最大化。内在性质：在有限的区域里，存在趋于无限的流域。

这个新函数不仅仅局限于经济学和农业应用，自变量也不仅局限于资金流和水流，还可应用于微管、血管、神经网络，计算机网络、电网、城市管网和道路分布等方面。

参考文献

(1)李宗尧，于纪玉《农田灌溉与排水》.北京：中国水利水电出版社，2003年.

(2)(3)(4)马列光《经济学新论：乘数、统计熵与国民收入》第34、44页、150页，北京：中国经济出版社2006年.

(5)王留运《低压管道输水灌溉工程技术》第20页.郑州：黄河水利出版社，2011年.