关键词：风力，发电机，风速，风向，有功功率，机械惯性，转动惯量，动力系统，微分方程

当前提高风电功率“短期”和“超短期”预测^[1]的可信途径有：㈠ 采用季风特性的空间相关性^[2]，㈡ 可信的组合预测^[1]；㈢ 缩短采样周期^{[1, 3]}；㈣ 更精确的风力发电机（以下简称“风机”）的“风速-功率”关系，等。

这里给出第㈣条思路的一些说明。

风机发出的有功功率P，是大自然的风驱动风机扇叶转动的结果。大自然的风速v(t)、风向，特别是风速v(t)，是风机出力的主要因素。一般认为，风携带的能量如下公式（1），即风功率是风速的3次方。这里参数A由叶片尺寸与形状决定的系数，ρ是空气密度。

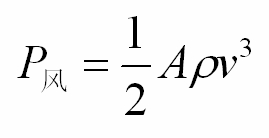              （1）

但是，必须说明：风机发出的电力有功功率P，不是P_风。因为风机扇叶受力转速对应的“有效风速”，即v(t)-u(t)，才是驱动风机发出电力的直接动力。如下公式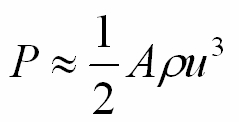（2）。

             （2）

这是因为“驱动风机的能量”来自扇叶：风吹动扇叶，扇叶带动发电机。当大自然的风速v(t)和扇叶折算速度u(t)一样时，风和扇叶是相对静止的（之间没有力的作用），亦即扇叶不会从风力获取能量。（类似的考虑还有风能利用效率与贝兹极限，The Betz limit - and the maximum efficiency for horizontal axis wind turbines ^{[4, 5]}）。v(t)和u(t)之间的差异，是形成风机实测“风速-功率”关系成为分散带的主要原因^[6-8]，如下图所示。

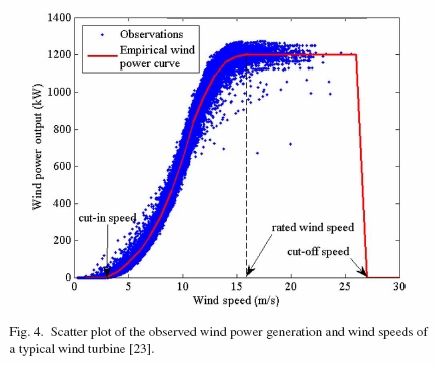
Li Pai 等2015年^[6]，第1598页，图4

因此，只要得到v(t)和u(t)之间差异，就可以获得更精确的风机“风速-功率”关系。将风机简化为一阶惯性环节^[9]，根据“定轴转动刚体转动惯量与转动角加速度的乘积，等于作用于刚体上的所有外力对转轴之矩的代数和”的基本原理，即可得到下述微分方程，即公式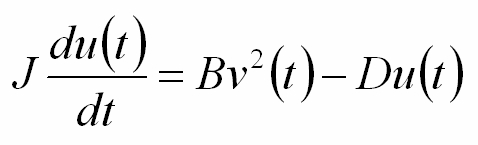（3）：

              （3）

这里J是风机的机械转动惯量，D表示阻尼（风机输出的有功功率、自身转动的阻尼等）。

通过求解该微分方程，就可以根据大自然的风速v(t)、风机的机械转动惯量J、阻尼D等，得到“有效风速v(t)-u(t)”，获得更精确的风机产生的电力有功功率P。

本文提出的是思路和原理（应当为“原创”）。今后结合实际风机，考虑更多其它相关因素，建立类似本文公式（3）的更精确的微分方程，只是一些具体的技术问题。是对我们思路的跟风。

我们尚未见到采用本文思路的他人研究。为保证我们（代表我国研究人员）在该问题研究上的“原创”优先权，特贴出本文。尽管我们不能保证这点。因为我们只能用汉语、英语查询相关资料。没有能力知道汉语和英语以外的语言是否有相关的公开报道。

参考文献：

薛禹胜，郁琛，赵俊华，等(Xue Yusheng，Yu Chen，Zhao Junhua，et al)．关于短期及超短期风电功率预测的评述(A review on short-term and ultra-short-term wind power prediction)[J]．电力系统自动化(Automation of Electric Power Systems)，2015，39 (6)：141-151．

杨正瓴，冯勇，熊定方，等(Yang Zhengling，Feng Yong，Xiong Dingfang，et al)．基于季风特性改进风电功率预测的研究展望(Research prospects of improvement in wind power forecasting based on characteristics of monsoons)[J]．智能电网(Smart Grid)，2015，3 (1)：1-7．

杨正瓴，张广涛，林孔元，等(Yang Zhengling，Zhang Guangtao，Lin Kongyuan，et al)．时间序列法短期负荷预测准确度上限估计(Upper limit estimating of short term load forecasting precision by time series analysis)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2004，16 (2)：36-39．

Betz's law - From Wikipedia, the free encyclopedia [OL]. https://en.wikipedia.org/wiki/Betz%27s_law

The Betz limit - and the maximum efficiency for horizontal axis wind turbines [OL]. http://www.wind-power-program.com/betz.htm

Li Pai, Guan Xiaohong, Wu Jiang, Zhou Xiaoxin. Modeling dynamic spatial correlations of geographically distributed wind farms and constructing ellipsoidal uncertainty sets for optimization-based generation scheduling[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1594-1605.

Miller L M, Brunsell N A, Mechem D B, et al. Two methods for estimating limits to large-scale wind power generation[J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(36): 11169-11174.

Banakar H，Luo C L，Ooi B T．Impacts of wind power minute-to-minute variations on power system operation[J]．IEEE Transactions on Power Systems，2008，23 (1)：150-160．

林卫星，文劲宇，艾小猛，等(Lin Weixing，Wen Jinyu，Ai Xiaomeng，et al)．风电功率波动特性的概率分布研究(Probability density function of wind power variations)[J]．中国电机工程学报(Proceedings of the CSEE)，2012，32 (1)：38-46．

杨正瓴

天津大学电气与自动化工程学院

2016-02-24