芯片中含有无数条线路和大量的半导体元器件，工作时若相邻线路中同时产生电流，在一定物理距离内两电流会相互干扰，产生热效应。通常电阻随温度升高而增大，升高的电阻又会产生更多的热量而升温。因此，芯片在工作时两相邻电流的相互干扰是一种非常有害的副作用。这种相互干扰的产生主要依赖于两电路间的距离。因此，纳米芯片在设计中如何规避同时性环路的相互干扰是一个重要的设计原则。在大于28或35纳米的芯片设计中这种规避原则并不怎么重要，但在14及14纳米以下的芯片设计中，这一原则不容忽视，并且芯片的纳米数越小，这一原则越突出。芯片的发展趋势能否越来越小，有没有极限？或者其中的理论基础是什么？本文从微观原子结构水平上进行探讨。

晶体结构或原子结构中的尺度都是以原子半径为基础的。根据相邻原子间的关系，原子半径可分为共价半径、离子半径、金属半径及范氏半径。其中无论哪种原子半径都是以相邻的两原子的核间距作为两原子半径之和确定的。不过，对于孤立的氢原子的玻尔半径则例外。玻尔理论是所有量子理论的入门通道，但它又仅属于经典物理学范畴。其中一个重要的原因是玻尔在推导原子半径时，只考虑了静电库仑引力，忽略了同等重要的洛仑滋力。因此，得到的玻尔半径比实际电子在定态时的最大轨道半径几乎小了一半，由于篇幅所限，将另文专门证明。虽然玻尔半径与氢分子中的共价半径大致相当，但在共价键能约束下，氢分子中的共价半径显然要比孤立氢原子中基态轨道半径小的多。

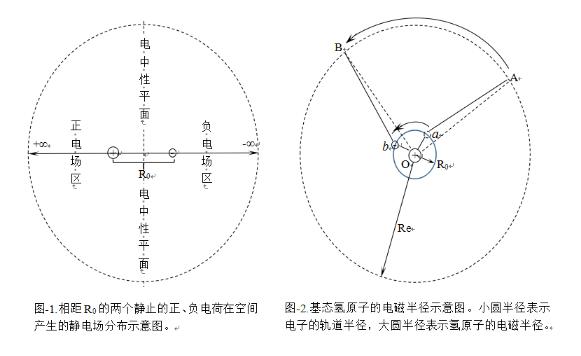
当把两个静止的正、负电荷放在相距为R₀的地方时，两个静止电荷产生的静电场分布如图-1所示。理论上由此产生的电场中性区只存在于两电荷连线的垂直平分面上。

我们现在考虑一个孤立氢原子的情况，其电子以大致光速的1/137(精细结构常数α)的速度绕原子的质心作轨道转动，原子核的运动可忽略。任何孤立的原子，在宏观上也都显电中性。但在原子内部，由于核外电子绕核电荷的动态轨道运动，在任一时刻的任一径向方向上都不会出现电中性。因此，对于任一孤立原子，必然存在一个宏观与微观的界定半径Re，原子内部的电磁波动（或电磁扰动）在时间和空间上相互叠加，在到达此半径处收敛为零。在大于Re的空间中测量时原子显示电中性，而在小于Re的原子空间中电场符号各处异性且呈动态变化。以Re界定的界面以外属于宏观时空，以内属于微观的原子内时空。我们将Re称为原子的电磁半径，它决不是电子绕核运动的轨道半径，更不是化学中大家熟悉的共价半径、离子半径、金属半径及范氏半径。因此Re是电子没有到达但它与核电荷的动态电磁波能够到达且能在时间和空间上相互叠加并收敛为零的一个半径。

如图-2所示，在基态氢原子中，设在时刻t₁电子在轨道中的a点，由于它的高速运动，相对论效应使它的运动空间受到压缩。它与核电荷产生的动态的正、负电场在A点处刚好相互中和并收敛为零。在t₂时刻电子到达b点，正、负电荷产生的动态电场的中和点在B处收敛为零。定态轨道运动必须满足驻波条件，也就是电子绕核运动完成一个周期，正、负电场产生的波动变化也必须要完成一个周期。因此在同一时间（t₂-t₁）内，驻波的波动从A到B转过的角度必须与电子从a到b转过的角度相等。我们得到孤长ab与孤长AB之比等于半径之比R₀/Re。即

又因为沿AB孤电磁波以光速c传播,若沿ab孤电子的运动速度为υ，则

υ/c = R₀/Re,

Re=R_0·c/υ=_,R₀/α=137R₀

式中的α为精细结构常数，R₀是氢原子基态轨道的最大半径，大致为玻尔半径的两倍。我们此处取R₀ ≈ 0.1 nm，因此

Re=137R₀ ≈ 14 (nm).

我们得到了孤立氢原子的电磁半径约为14 nm，若两个固定的孤立氢原子间距离超过28 nm，则基本无电磁干扰。若两个孤立氢原子间的距离小于28 nm，则难以避免相互间的电磁干扰。当然，在光电管中的氢原子或氢分子的热运动使它们相互碰撞，不可能得到固定的28 nm.的间隔，因此它们都有参与化学反应的活性。

量子力学是一门数学，数学是一个工具，所得结果只有根据实际情况进行取舍之后才能赋予真正的物理意义。量子力学处理氢原子体系时引入的主量子数n是从1开始的自然数，最大可到+∞。例如，氢原子光谱的波长可用下面的公式计算：

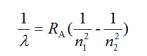
式中的里德堡常数R_A=1.097×10⁷m^-1，n₁=1，2，3，4，……，∞，其中每一个数值代表氢原子的一个光谱系。例如1，2，3，4，5，6分别代表莱曼系、巴耳末系、帕邢系、布拉开系、芬德系和汉弗莱系。式中的n₂=n₁+1，n₁+2，n₁+3，n₁+4，……，n₁+∞，其中每个数值代表该光谱系中的一条光谱线。从纯数学角度考虑，氢原子应该有无数光谱系，每一光谱系又有无数条光谱线。但实际上氢原子的光谱系及其相应的谱线都没有那么多，有名的氢原子的光谱系就那么6个，最多不超过12个；同样，每个光谱系中的谱线也就那么六、七条，最多不超过12条。因为当n等于12时，n²=144，与该能级相对应的轨道半径r_n=r₀n²=144 r₀. 若r₀取0.1nm, r_n已经达到了14.4nm的半宏观尺度。从另一方面考虑，精细结构常数的倒数也仅有137，137<144.因此，氢原子中电子跃迁的最高能级不超过12。在12以内，能级越高，相邻的光谱系及相应的相邻谱线越靠近，越趋于简并化。可见，在量子力学中得到的+∞，在实际物理体系中未必是一个大到可怕的数字。

现在我们来考虑存在于固体表面的电磁干扰层的厚度。通常固体的规则表面以晶体作为研究的对象。晶体表面各原子的价层电子运动产生的电磁干扰层从表面向外延伸，它们不再是单个的球面波，而是与固体表面大致平行的一个动态的面。芯片的主体成分是高纯的晶态硅和构成半导体元件的掺杂原子，如硼原子等。硅的共价半径为0.111nm, 硼的共价半径为0.082nm。因为它们的共价半径都是实验测量数据，不存在像玻尔理论中玻尔半径被少算的问题。另一方面，硅、硼原子中价电子比氢原子中电子感受到的有效核电荷要大，再考虑到氢原子是孤立体系，晶体中硅或硼原子中的价电子的轨道半径也不会比氢原子的基态轨道半径大多少。因此，我们可以近似将14nm作为芯片制作中的电磁干扰层厚度。

对于固体材料，延伸到表面以外的大致14纳米厚的电磁干扰层对材料的表面性质的影响是至关重要的。上世纪后期发展起来的纳米材料就是很好的例子。人们将直径位于几纳米到几十纳米的颗粒或纤维统称为纳米材料。由于几纳米到几十纳米的曲率半径与电磁干扰层厚度相当，所以纳米材料具有特别高的化学活性。其物理化学性质与同种的大块材料具有截然不同的差异。

芯片在工作时内部被赋予了大量的瞬时导通环路。根据逻辑门关系，环路可分为同时导通环路和非同时导通环路。例如电脑在点击关机键时会弹出关机、睡眠、重启等多个选项，这些选项都是并列的，与它们相关的导通环路间都为非同时导通环路。工作时非同时性导通环路间的电磁干扰通常被回避，但物理上相邻的两个同时导通环路间的电磁干扰是不能避免的。有电磁干扰就有热效应，芯片工作时就会发热，不但增大电能消耗，还可能影响指令的正常运行。因此在设计制造时保持足够大的相邻环路间的物理距离，是避免电磁干扰的基本方法，例如制造28纳米或35纳米以上的芯片。只要避免制造过程中出现的缺陷，在考虑电磁干扰方面28纳米以上的芯片是比较安全的。

大尺度的芯片虽然能避免相邻环路间的电磁干扰，但长的运行环路导致运行速度放慢，内置元件密度减小，因此，实际上人们在不断追求越来越小尺度的芯片，从14纳米、7纳米到5纳米，电磁干扰的影响依次增大。能够避免这种电磁干扰的办法，是在芯片设计中，通过数学计算，将工作时可能出现的瞬时同时导通环路置于物理距离更大的位置。将工作时瞬时永不同时导通环路放在最近的物理邻居位置，能够避免工作时同时导通环路间的电磁干扰。