按照大气压强公式我们推导出大气的厚度P=水银pgh=大气pgh，大气h=水银pgh÷大气pg=(13.6×10³kg/m³×9.8m/s²×0.76m)÷(1.225kg/m³×9.8m/s²)＝8437.55102040816m。

从压强公式中我们计算出一个标准大气压所产生的大气厚度8437.55m，那么以8437.55m半径的圆形大气质量是多少？按照一个标准大气压常温常压下计算，假设中心真空部位以1m³，按照标准常温常压下大气质量1.29千克/m³。

首先计算半径r = 8437.55米的球体体积V总：

 V总=4/3πr³

=4/3×π×8437.55³

≈2.49×10¹²m³

已知真空部位体积是1立方米，那么包含大气部分的体积

V = V总 - 1

=2.49×10¹²m³-1m³

又因为标准大气压、常温常压下每立方米大气质量约为1.29千克，所以该区域大气质量M为：

 M=1.29×(V总 - 1)

=1.29×(2.49×10¹²- 1)

=1.29×2.49×10¹² - 1.29×1

=3.2121×10¹²- 1.29

≈3.2121×10¹²千克（减去的1.29相对极小可忽略不计）

地下8公里处的压强压力所产生的质量计算可看作是8000×3.2121×10¹²千克≈25696.8×10¹²千克。以上是粗略计算，一些数据的获取来自网络，测量数据不同不是关键，主要了解其原理。

由真空得到大气厚度值以及计算大气质量，对照地球模式，地球与托里拆利实验模式类似，这里得出一个结论；不管是海水、岩浆、岩石或者是空气，调整压强压力变化的是地球，压强是以地球上的任意一个点到地球中心画圆，而圆线上的任意一个点的压强测量数据必定与圆线上的其他点测出的压强相等，也就是说圆线上的压力值必须相等，否则地球不稳定，我们可以依据这个测量数据以及计算结果得到常数，地球常量为参照数据。

我们再来观察托里拆利实验，

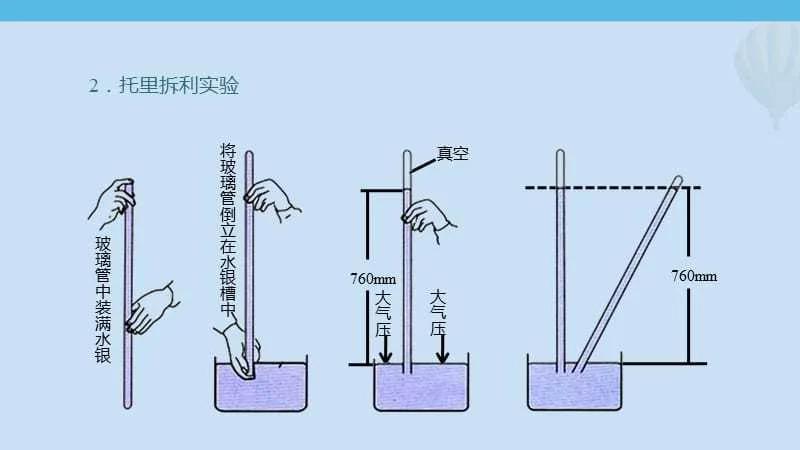
不论玻璃管怎么倾斜，液位高度不变，哪怕玻璃管不是直管，弯曲并加长，只要有一定的斜坡，最终测量垂直高度同样是760mm。从实验再回到地壳的现状，地壳内溶洞错综复杂，终究不会如同玻璃管一样直来直去，弯曲盘旋都有可能，然而这不影响形成以真空环境为条件的单独压强空间结构。

以真空为条件的单独压强空间结构以真空为中心，形成一个近似圆形的质量空间，这个质量空间由于无法像地球一样运动，调动水源，调动大气来维持平衡，所以在压力不均衡的情况下发生真空爆破，这是地震的起源。

如何获取数据作为参数来计算地震时间？建立全球联网的地震数据中心；第一，我们要得到地球的大气压强常数，这个常数要精确，作用是了解以地球中心点到四面八方的准确数据，这个数据为常数。第二，参照以前的地震事件，掌握全球测量地震的气压数值与地球常数进行比对，求出压力差，计算出地震中心点的压强，这个压强与震烈作为数据保存。第三，由于形成真空需要一定的时间，并且地壳中的液态为岩浆，所以形成真空的过程属于气压不稳定的时间段，掌握气压不稳定的时间段很重要，形成真空的过程所造成的影响可以使河水井水水位下降，大气流动加速，云层以鱼鳞状汇聚，这些都有可能发生地震，然而发生地震需要的是压力不稳定，所以获取压强不稳定值至关重要。第四，需要计算不稳定值的压强落差幅度和时间差，压强落差幅度与时间差是关键，这里有两种现象存在，一种是由慢到快，一种是由快到慢，由快到慢地震的发生概率几乎为零，原因是真空压强空间结构周围整体质量得到了控制，也就是说水和大气填补了局部质量，使真空压强空间结构获得稳定。由慢到快地震的发生概率很大，毕竟大气质量比不上水的质量大，如果水的质量不能让真空压强空间结构获得稳定，那么大气压强就会不稳定，容易发生地震。

为便于直观思考请仔细观察下图；地球大气压力与托里拆利实验融合图

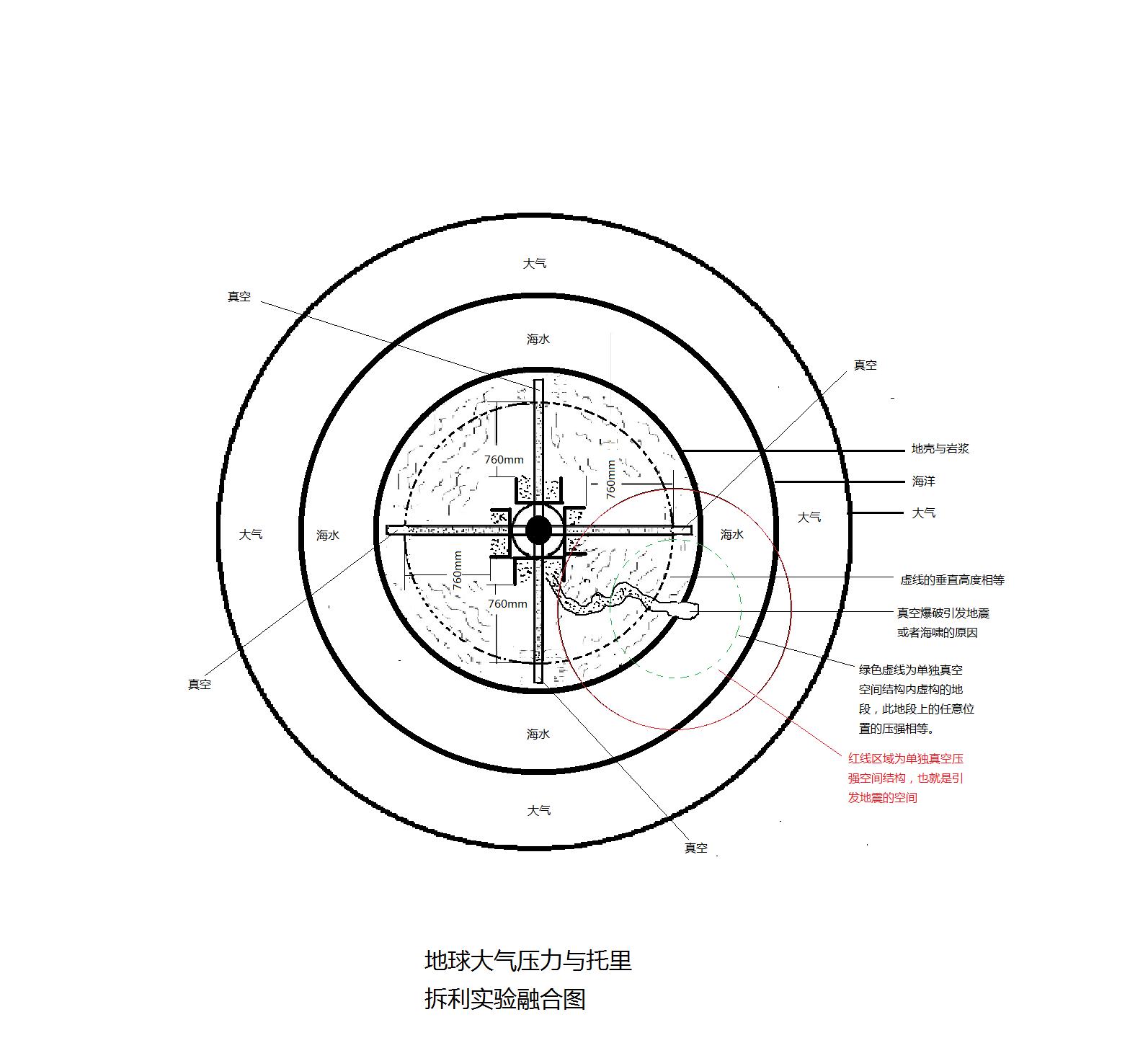
单独真空压强空间各个地段的压强同样依照各个地段到真空部位画圆，圆形线上的压强相等，由于单独真空压强空间内的压强数值与地球的整体常数不吻合，所以我们可以利用数据的等差关系获得时间差以及压强落差幅度，并且通过参数对比能够准确做到提前预报地震。