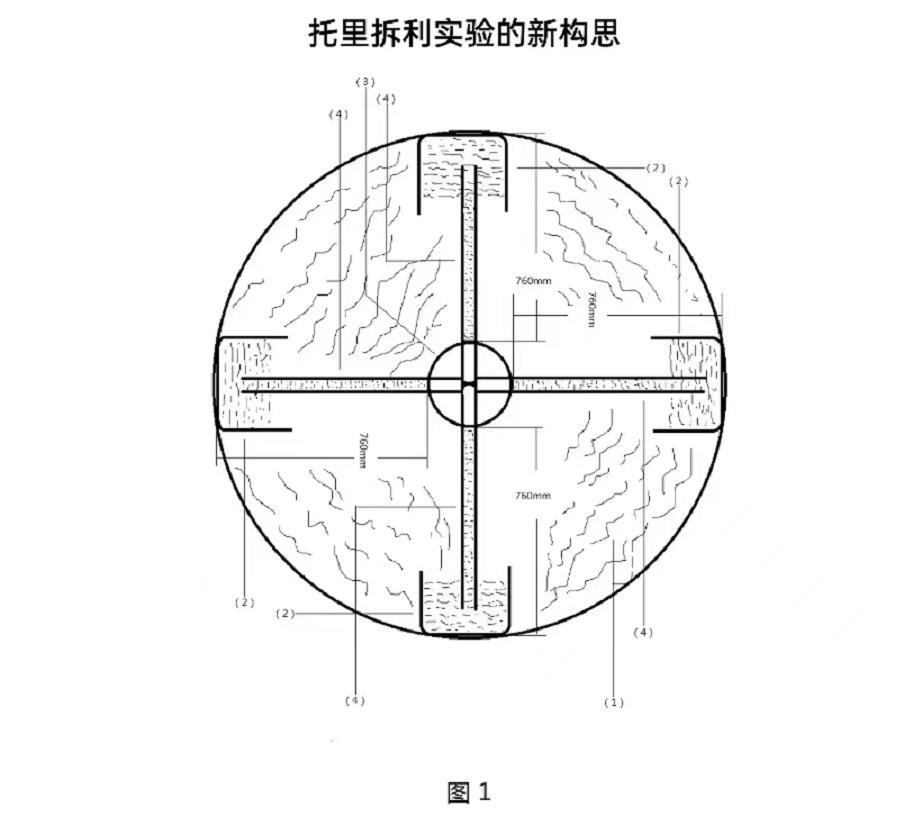
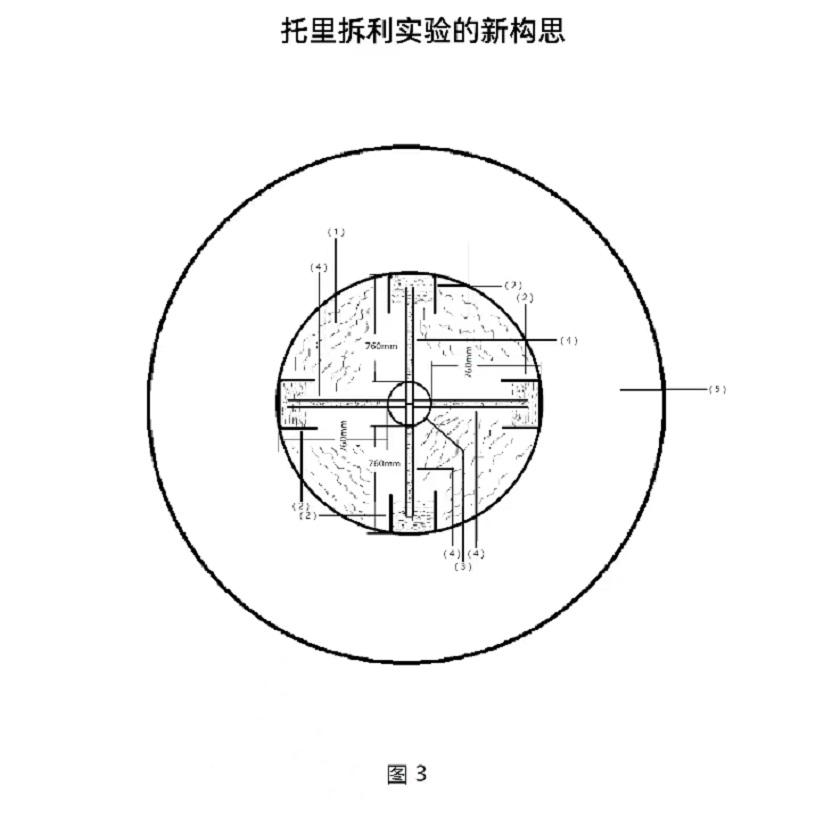
以上图1、图3是托里拆利实验大气压强简易改进图

从压强公式中我们计算出一个标准大气压所产生的大气厚度，大气厚度8437.55m相对于玻璃真空管的横截面积形成一个环绕式的大气厚度，这是压强公式中大气的常量，由P=pgh=水银pgh=大气pgh中获得，由真空得到大气厚度值让我们打开新的知识，对照地球模式，地球与真空所获得的环绕式大气相等，而在地球的内部岩浆溶洞必然也是错综复杂，岩浆密度是2500至3100千克/m³，水的密度是1000千克/m³，大气密度是1.29千克/m³，海水深度10米处压力约等于一个标准大气压，深度100米压力约等于10个标准大气压，深度1000米约等于100个标准大气压，深度10000米约等于1000个标准大气压，而最浅的大地震1976年唐山大地震，震源深度约8公里，虽然只有8公里，但是震级强烈，能够引发这么强烈的地壳运动，除了真空性质之外没有其他方式可以引发地壳运动，因为岩浆溶洞如同托里拆利实验中倒置于水银中的真空玻璃管，只要岩浆溶洞形成真空，那么在近似800个标准大气压下所承受的压力只要超出岩浆溶洞的承受范围，那么就会引发真空爆破，真空爆破是引发地震时地壳运动的主要原因。找到引发地震的原因，那么我们就能利用常数来推演各地的地震时间，提前预报地震是可以实现的，因为真空爆破之前有一个真空形成过程，而真空形成过程是局部压力压强形成环绕式的过程。我们再观察托里拆利实验，不管真空管的粗和细，只要倒置过来就能产生相同的一个标准大气压强，大气的厚度与真空管的横截面积有关，地震与大气厚度以及横截面积的大小成正比，此中的微小变化取决于是否形成环绕式的局部真空性质，由于地球岩浆始终处于流动状态，海水和大气同样，流动是地球的整体环境，而在这个整体环境中如果出现局部真空，那么就会产生一个近似圆形的地震环境，这个地震圆形环境的主要特征缘于海水和大气的流动，海水让力保持了一个平衡状态，而大气给我们一个直观检测数据，有了数据就能演算出地震位置以及所受的压力大小。若要计算地震时间那么就需要掌握地震环境中的出入流速，流速越大其地震环境中的压强就会越大，达到溶洞爆破的临界值就是地震的准确时间。