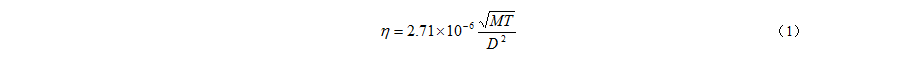我在《太阳系角动量分布异常的定量新解释》一文中,算出的原始太阳星云动力粘度为2.02×105Pa·s;它比地球上任何已知气体及液体的粘度都高得不可比拟,那样稀薄的气体竟能产生如此高的粘度,凭直觉和经验来判断,是绝对不可能的。当我联想到地球大气外层也有电离层,照理现在发射同步卫星的火箭绝无可能穿过粘度如此之高的电离层;但实际上不但穿过了而且也未发现阻力有什么明显变化。由于存在这种强有力的反面证据,而又根本无法用实测粘度来验证,我曾一度绝望地想放弃有关论证与计算。但我在本栏目“新观点新学说沙龙”的讨论中,看到张开逊先生的发言很受启发,并打消了上述想法,不再仅指靠实验来解决理论论证问题。
张先生指出,近代科学出现之初,人们笃信“实验是自然科学的基础”,通过实验能发现自然的奥秘并建立理论;但这种观点从哲学层面上考虑是有问题的,因为通过实验固然会发现新的现象,发现自然的奥秘,但是要发现具有普遍性的、预测性的理论需要无限多个新的事实才行,而任何人所做的实验,所涉及的自然对象都是有限的,故不可能通过实验发现新的理论。牛顿和爱因斯坦都曾由笃信传统看法中逐渐转变过来,后来他们都说,“只靠经验和实验要获得理论,是不可思议的”。所以我才决定继续将上述论文撰写完毕。因该稿篇幅太长,无法投送本栏目;其缩写稿《原始太阳星云塌缩过程的理论分析与计算》一文已在本栏目发布。
现撰写本文的目的就是想进一步证明,氢的电离气体具有极高粘度的可能性,所以只计算氢离子浓度较高的地球高层电离层的粘度,及进行相关论证。
1.地球电离层动力粘度的计算
据报导[1],在地面1000km高度以上的电离层中主要成分是H+,高于2800km则几乎为H+所独占。因该处物质密度也很低,其动力粘度同样可按如下理论公式来计算[2]:
式中 η:动力粘度(Pa·s); M:气体克分子量;T:气体绝对温度(K);D:粒子直径(埃)。
据介绍,它是按组成气体的粒子为弹性球的模型推算出来的,其计算误差约为10%。
因氢离子可看作质子,其质量约为氢分子质量的一半,其克分子量M可取为1;其直径约为1.6~1.7×10-15m;等于1.6~1.7×10-5埃;约比氢分子小5个数量级。高层电离层的温度找不到确切的数据,好在它对粘度计算结果的影响很有限,故这里假设为300K。将上列数据代入(1)式可算得η=1.62×105Pa·s。
2.对计算结果的讨论一论证
以上计算结果是按经典的气体粘度计算公式算出的;该公式是麦克斯韦从纯理论基础上推导出来的并为后来的实验所证实,这被认为是分子运动理论的光辉成就之一,所以我们无法怀疑它的正确性。星云物质密度虽很低,但密度低不能成为怀疑它粘度高的理由,理论分析证明,在给定体积内增加组成气体的粒子数,虽能增加动量携带者的数量,但因单位体积内粒子数增加一倍时,其自由路程相应要缩短一半,故任一携带者的动量平均值,同样只有它下一次碰撞地点平均动量的一半,也就是说它们的动量交换效率降低了;所以才得出粘度与密度无关的计算结果。此外,从(1)式可以看出,粘度与粒子直径D的平方成反比,而氢离子的直径比氢分子小5个数量级,这是使计算粘度特别大的决定性因素。在地球表面环境下绝对找不到由如此小直径粒子组成的气体,所以凭感觉和经验也绝对无法判断其计算是否正确。那么,火箭能无阻挡地穿出电离层又作何解释?下面来通过定量计算来论证这个问题。
3.火箭穿过电离层摩擦阻力的计算
要用解析法精确计算火箭通过电离层的摩擦阻力是非常复杂和困难的,至今还未找到这种方法。好在这里计算结果只要不出现成倍的偏差就足够了,所以要进行定量计算还是容易办到的。
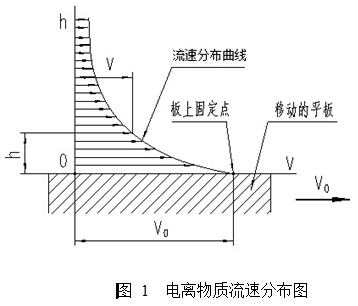
假设火箭在单位面积上所受电离层摩擦阻力与相同面积的平板以相同速度在在电离层中移动所受阻力相等,那么电离物质流动的速度分布将如图1所示。图中座标系在瞬间是静止的,当单位面积的平板相对该座标系以速度V0移动时,电离物质靠近板面的流速应近似与平板移动速度相同;由于火箭前进带动电离物质前进的惯性力要抵消部分摩擦剪切应力,所以该应力要随h的增大而逐渐降低,从而使速度梯度dV/dh的绝对值也逐渐降低。
为进行有关计算时需先判断在上述条件下,火箭相对电离层的流动是层流还是紊流,故需计算其雷诺系数。由于电离物质的动力粘度非常大,其密度又非常小,而其运动粘度又等于前者除以后者,故其量值会大得惊人。但雷诺数又与运动粘度成反比,故它会小得惊人。大量试验已证明雷诺数大于2000时才会出现紊流,故无需再作定量计算就已证明,火箭相对电离层的流动一定是层流。因此根据牛顿公式,平板附近的空气中所产生的剪切应力可按下式计算:
据报导[3],在1000km高度上,电离层的电子密度为105个/cm3,那么,氢离子数也应与此相等,它除以阿伏伽德罗常数,可近似求得其密度为1.66×10-19g/cm3=1.66×10-16kg/m3。另设火箭长度为20m,V0=8km/s=8000m/s。将上列数据代入上式可算得τ0=0.48Pa。这说明火箭每平方米面积上受到的摩擦阻力仅为0.48N,完全可忽略不计。究其原因,就是由于该处电离层密度极小;计算表明,火箭前进即使带动8千万立方千米的电离层物质加速前进,也只相当多带动1kg物质加速前进所受的惯性阻力。所以不能因为感觉不出阻力的变化就以它来否定上述粘度计算结果的正确性。也由此可见,光凭感觉和经验而不作定量计算来作判断,产生的偏差和产生误判的可能性有多么巨大。
(11)式右端根号下,分子各项参数对剪应力τ0形成的机理都比较容易理解,但在分母中出现的参数L则有所不同,故需作一些解释。火箭前部将带动周围静止流体向前行,故流体与后部的相对速度会降低,从而会降低摩擦剪应力τ0。这种效应将随着L的加大而增大,并已被列车及汽车行驶的测算结果的对比所证实。
4.结语
人们常认同“眼见为实”的看法,但在科学探索中,该观点不一定可靠。例如本文推导的(11)式就推翻了凭感觉和经验作出的判断,这种实例不胜枚举,也可从我与赖柏林先生的争论中找到很多实例。可见只有提高到理论高度来研究自然现象,才能深刻理解其真象和实质。故殷切希望有些只重实践不重理论的业余科研爱好者从这种探索方法中转变过来。
参考文献:
[1] 百度百科,地球电离层,2010-05-05
[2] 钱学森,物理力学讲义,科学出版社,1962(P308)
[3] 百度文库,电离层结构,2012-4-13