水质基准是指水环境中污染物不会对特定水生生物产生不良影响的最大可接受浓度或剂量。水质基准为环保部门制定水质标准、评价水质以及进行水质管理提供科学依据，促进保护生物多样性和生态系统多功能性。物种敏感分布法是一种统计外推技术，通过拟合污染物毒性数据，推导出保护水环境中，任意比例物种不受污染物影响的有害浓度。通常计算出保护95%物种不受影响的污染物浓度(HC₅)，将HC₅除以环境评估因子(一般取值为1-5)即为水质基准。由于物种敏感分布法既简便又准确，而被广泛应用于水质基准推导中。中国、欧盟、荷兰、澳大利亚和新西兰等多个国家将物种敏感分布法作为推导水质基准的标准方法。物种敏感分布法的关键在于模型的选择，目前使用的模型以参数类为主，包括：正态分布、对数正态分布、逻辑斯谛分布、对数逻辑斯谛分布、Burr-Ⅲ分布、对数三角分布、威布尔分布等。非参数法主要有： Bootstrap、Monte Carlo法等。

1物种敏感分布

物种敏感分布法最初是由Kooijman(1987)提出。后经很多学者改进，广泛应用于水质基准推导中。不同种属的生物由于生理构造、行为特征不同，对同种污染物的敏感性存在差异。物种敏感分布法假设随机挑选的物种能够代表整个生态系统的群落结构，并认为污染物引起生物不适的毒性数据遵循某种数学分布。物种敏感分布曲线一方面可以从污染物浓度出发得到受影响物种的百分比用于环境风险评价。另一方面可以推导保护生态系统中任意百分比物种不受污染物影响的水质基准。物种敏感分布法对数据的充分利用程度、随机抽取物种对生态系统的代表性和简便的操作方法，使其成为推导水质基准的主流方法。且有研究证明物种敏感分布法是一种实用、直观的工具。但由于物种敏感分布法是基于数据和模型的外推方法，数据的质量和分布模型的选择都会影响最终的基准值。

数据方面，物种敏感分布法中使用的数据类型主要有：总数据、加权平均值、算术平均值与物种最敏感值。使用加权算术平均值进行拟合，能够在保留物种内差异的同时给予每个物种相同的权重。为方便起见，通常使用数据的算术平均值，并对数据进行对数转换，来降低原数据之间较大的差值。为了充分发挥物种敏感分布法随机选择物种对生态群落的代表性，以及为了保证模型拟合曲线的精确度，在推导水质基准中提出毒性数据最小量的要求。欧盟规定数据量应至少包含8个分类群中的10个物种，美国使用的是3门8科的最低数据要求，我国则规定数据应在3个营养级范围内涵盖6个不同生物类群中的10个物种。另外当数据量较少时，物种敏感分布法往往不能给出精确的拟合曲线。虽然扩充毒性数据集能够减小HC₅的误差，但数据集越大满足置信度需要的最小样本量越多。因此应避免过度补充数据集，而增加拟合的不确定性。由于没有一种可用于所有污染物数据拟合的普适模型，在使用物种敏感分布法推导基准时经常出现争议。因为每种模型的基础理论不同，在面临相同的条件时会出现拟合差异。使用不同的参数模型会得到不同的物种敏感分布曲线，推导出的水质基准存在偏差，数据量越少，差异越明显。使用同一组毒性数据，不同的模型拟合外推得出的基准值差异在一个数量级甚至更大。这是由模型本身的差异导致的。模型不同则函数不同、参数估计方法不同，从而在拟合数据时会出现一定的内在偏差、误差和不确定性。毫无疑问，这将会影响水质标准的精确程度以及保护生物多样性的效率。

2物种敏感分布法中典型的几种拟合模型

2.1正态分布

若随机变量X服从一个数学期望为μ，方差为σ2的正态分布，记为N(μ, σ2)。符合正态分布的数据集的特点就是对称和集中，极端数据少而中正数据多。物种敏感分布曲线拟合之前需要将对数转换后的数据进行正态性检验。检验一组数据是否符合正态分布有图形法和统计法。分位数-分位数图(Quantile-quantile plot, QQ-Plot)和概率图(Probability-Plot, PP-Plot)用于判断样本是否近似某种分布或者判断两个样本是否来自同一分布，若样本符合正态分布，则图示数据点应集中分布在y = x直线上。统计法中包括：S-W检验(Shapiro-Wilk test Test)、K-S检验(Kolmogorov-Smirnov Test)、A-D检验(Anderson-Darling Test)、T检验(Student`s Test)、卡方检验(Chi-Squared Test)等。其中小于3000个数据时以S-W检验为准，大于3000时以K-S检验为准。T检验适合于小样本(<30)的正态检验。

如果一组数据受多个独立因素共同影响，但没有一个主要因素，那么这组数据倾向于正态分布。正态分布的公式为：

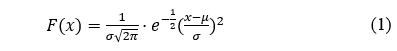
式中F(x)为累积概率，%；x毒性数据， μg/L；μ为毒性数据的平均值，μg/L；σ为毒性数据的标准差，μg/L。(本文公式中所有相同符号含义与单位均相同)。

2.2对数正态分布

如果随机变量X服从正态分布，则exp(X)服从对数正态分布。对数正态分布也是一类描述增长的函数，增长开始时，对数正态分布与正态分布相似，但随着时间推移，对数正态分布明显向上提升，具有很长的右尾，属于右偏态分布。如果影响变量的因素可以看作是各独立因素乘积的结果且没有一个主要因素，则变量倾向于服从对数正态分布。

很多毒性数据可能来自不同的实验室，跨时间跨地域收集的，同一个物种的毒性数据也会存在很大的差异。因为对数正态分布有适当的偏度、较重的右尾和容易计算的参数，所以能够很方便的描述这些数据。对数正态分布的公式：

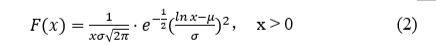
一般具有极端值的数据，如单日最高温度、每周的最大降雨量等的数据倾向于服从对数正态分布。对数正态分布曲线的尾部衰减较快，较窄的尾部对数据的适用性差。上世纪就有学者将对数正态分布用于风险评估。

逻辑斯谛分布是一种双参数连续型概率分布与正态分布非常相似。19世纪上半叶，比利时数学家Verhulst在人口统计工作中首次提出逻辑斯谛增长函数，主要用于描述客观事物的增长模式。在标准差相同时，与正态分布相比，逻辑斯谛分布具有更大的峰值和更厚的尾部，属于尖峰、厚尾型分布。但逻辑斯谛分布容易出现极端值，在原函数中加入两个形状参数得到广义逻辑斯谛分布，能够详细地描述曲线的尾部。 

逻辑斯谛分布是体现了“有限环境空间”的概念，更接近环境中种群的实际增长状态。逻辑斯谛分布模型的表达式为：

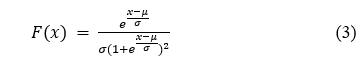
逻辑斯谛分布能够直接计算出任意百分位对应的浓度值，如计算对数HC₅时可表示为：ln(HC₅) = μ-1.6234σ。相比于正态分布，逻辑斯谛分布的置信区间计算更复杂，置信度只能达到单尾95%或双尾90%，达不到统计意义上双尾95%的要求。从数学上看逻辑斯谛分布只是个经验方程，并非逻辑推理而得。逻辑斯谛分布与正态分布的拟合效果相近，但逻辑斯谛分布适用的数据类型更广，拟合小数据集精确度更高。 

2.4对数逻辑斯谛分布

顾名思义，对数逻辑斯谛分布变量的对数服从逻辑斯谛分布。对数逻辑斯谛分布类似于对数正态分布，但对数逻辑斯谛分布的尾部更厚，属于右偏厚尾型分布。对数逻辑斯谛分布能够很好的处理原数据缺失的情况，可操作性更强。其公式如下：

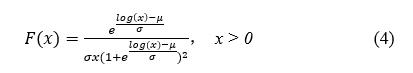
对数逻辑斯谛分布与对数正态分布具有相似的拟合效果。但对数逻辑斯谛分布有更长的尾部，拟合结果更保守。对数逻辑斯谛分布能够准确的处理小数据集(10~15个数据)。与其他分布相比，对数逻辑斯谛分布往往能得到更稳定的HC₅。对数逻辑斯谛分布因其强适用性与稳定性，而被广泛使用。

2.5伯尔三参数分布

Burr-Ⅲ分布是一种灵活性高，适用性强的三参数连续分布模型。Burr-Ⅲ分布在平面上覆盖了巨大的区域，涵盖了几种常用的分布，如：伽玛分布、威布尔分布、正态分布、逻辑斯谛分布等。Burr-Ⅲ分布具有较大的偏斜度和峰度值，几乎可用于拟合任何给定的单峰数据集。

将对数逻辑斯谛方程进行变换，

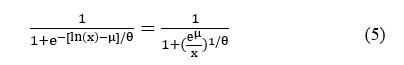
就得到Burr-Ⅲ的参数方程：

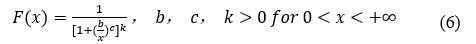
公式中b = e^μ， σ = θ·π/√3，c = 1/θ， k是新的参数。当k = 1时， Burr-Ⅲ分布为对数逻辑斯谛分布。

每个参数都有明确的意义，b是尺度参数，c是形状参数， c和k决定曲线的位置，尺度参数b使Burr-Ⅲ模型更灵活多样;当c > 1/k时曲线是单峰函数，当c≤1/k，曲线是L型函数。Burr-Ⅲ分布适合拟合呈扁态、厚尾型的数据，能够准确的分析和预测曲线高累积概率区域。但Burr-Ⅲ分布的计算分析复杂，数据转换不确定性高，尤其在处理小数据集(5-7个)时存在较大误差。

Burr-Ⅲ模型最先在澳大利亚和新西兰的环境风险评估和环境质量研究中推荐使用。Burr-Ⅲ模型在多种污染物的物种敏感曲线拟合中表现出高精确性，是使用较多的参数模型。

3五种模型的差异性对比

表1  五种模型主要差异性比较

4模型的应用案例分析

以我们之前研究的镉（Cd）的水生生物急性毒性数据为案例，采用文中提到的5中拟合模型，分别对之前研究中镉的种平均毒性数据进行了物种敏感分布拟合。结果如图1所示。

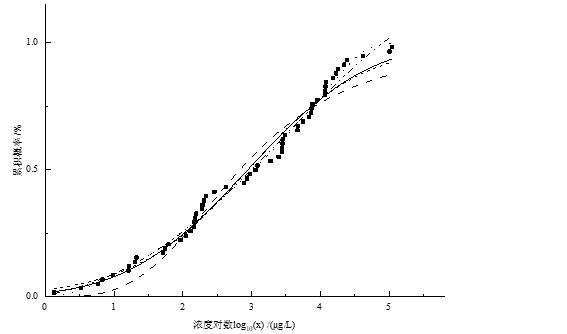
·-··-正态分布；——对数正态分布；  - - - - 逻辑斯谛分布；— —对数逻辑斯谛分布；····Burr-Ⅲ分布。

图1  基于五种参数模型所构建的镉的物种敏感分布曲线。

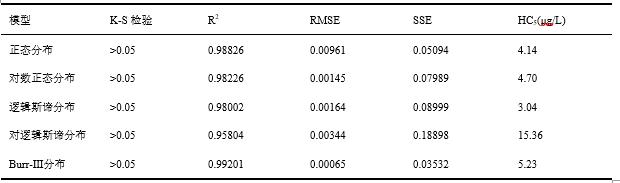
结果发现：Burr-Ⅲ曲线与原始数据吻合度最高，对数逻辑斯谛曲线与原始数据离散程度最大。Burr-Ⅲ在曲线整个阶段都表现出高精确度的拟合效果，对数正态分布、逻辑斯谛分布、正态分布在仅低累积概率拟合效果较好。另外，采用决定系数(R2)、均方根(RMSE)、残差平方和(SSE)，三个参数对模型的拟合优度进行统计学检验(表2)，统计结果表明，五种模型均通过K-S检验，且Burr-Ⅲ分布是最优模型。

表2 五种模型拟合优度评价指标计算结果

5结论

物种敏感分布法是一个实用、直观的工具，模型的选择是物种敏感分布法中最关键和核心的问题。物种敏感度分布拟合中，每个模型都有最合适的使用条件，无论选择哪种模型，都应该充分描述数据的信息，确保拟合出的物种敏感分布曲线在统计学上具有合理性，可靠性。最直接的方式是使用多种模型，选择拟合优度最高的模型。因此，基于本文中介绍的五种物种敏感分布拟合模型，我们提出以下两条建议：(1)使用正态分布处理高度集中、对称分布的数据集；对数正态分布处理含有极端值或数据量大的数据集;逻辑斯谛分布处理厚尾型数据集；对数逻辑斯谛分布处理数据间差值大或数据量小的数据集；Burr-Ⅲ分布处理呈扁态、厚尾型数据，且数据量必须大于8的数据集拟合。(2)重点研究低累积概率处，可选择对数正态分布、逻辑斯谛分布；重点研究高累积概率区域，使用Burr-Ⅲ分布。

参考文献：

[1] 吴丰昌，冯承莲，张瑞卿，等. 我国典型污染物水质基准研究[J]. 中国科学：地球科学, 2012, 42(05): 665-672.

[2] 周启星. 环境基准研究与环境标准制定进展及展望[J]. 生态与农村环境学报, 2010, 26(01): 1-8.

[3] SOLOMON K R, BAKER D B, RICHARDS R P, et al. Ecological risk assessment of atrazine in north american surface waters[J]. Environmental Toxicology and Chemistry, 1996, 15(1): 31-76. 

[4] 陈丽红，张瑜，丁婷婷，等. 红霉素水生生物基准推导和对中国部分水体生态风险初步评估[J]. 生态环境学报, 2020, 29(08): 1610-1616.

[5] ANZECC A. Australian and New Zealand guidelines for fresh and marine water quality[J]. Australian and New Zealand environment and conservation council and agriculture and resource management council of Australia and New Zealand, Canberra, 2000: 1-103. 

[6] HJ831-2021 淡水水生生物水质基准制定技术指南[S].

[7] CANADIAN COUNCIL of RESOURCE and ENVIRONMENT MINISTERS (CCME). A protocol for the derivation of water quality guidelines for the protection of aquatic life[R]. Ottawa: CCME, 2007.

[8] 吴丰昌，冯承莲，曹宇静，等. 锌对淡水生物的毒性特征与水质基准的研究[J]. 生态毒理学报, 2011, 6(04): 

367-382.

[9] 吴丰昌，冯承莲，曹宇静，等. 我国铜的淡水生物水质基准研究[J]. 生态毒理学报, 2011, 6(06): 617-628.

[10] FENG C L, WU F C, ZHAO X L, et al. Water quality criteria research and progress[J]. Science China Earth Sciences, 2012, 55(6). 

[11] STEPHAN C E, MOUNT D I, HANSEN D J, et al. Guidelines for deriving numerical national water quality criteria for the protection of aquatic organisms and their uses[M]. US Environmental Protection Agency Washington, 1985.

[12] TRAAS T P. Guidance document on deriving Environmental risk limits[R]. Bilthoven, the Netherlands: National institute for public health and the environment (RIVM), 2001.

[13] ECB. Technical Guidance Document on Risk Assessment-Part Ⅱ[R]. Italy, Ispra: Institute for Health and C onsumer Protection, 2003.

[14] VAN V P, TRAAS T, WINTERSEN A, et al. A program to calculate hazardous concentrations and fraction affected, based on normally distributed toxicity data[J]. National Institute for Public Health and the Environment (RIVM), Bilthoven, the Netherlands, 2004.  

[15] NEWMAN M C, OWNBY D R, MEZIN L C A, et al. Applying species-sensitivity distributions in ecological risk assessment: Assumptions of distribution type and sufficient numbers of species[J]. Environmental Toxicology and Chemistry, 2000, 19(2): 508-515.

[16] WAGNER C, LOKKE H. Estimation of ecotoxicological protection levels from NOEC toxicity data[J]. Water Research, 1991, 25(10): 1237-1242.

[17] ALDENBERG T, SLOB W. Confidence limits for hazardous concentrations based on logistically distributed NOEC toxicity data[J]. Ecotoxicology and environmental safety, 1993, 25(1): 48-63.

[18] SHAO Q. Estimation for hazardous concentrations based on NOEC toxicity data: an alternative approach[J]. Environmetrics, 2000, 11(5): 583-595.

[19] MOREIRA R A, MANSANO A D S, ROCHA O. The toxicity of carbofuran to the freshwater rotifer, Philodina roseola[J]. Ecotoxicology, 2015, 24(3): 604-615.

[20] VAN STRAALEN N M. Threshold models for species sensitivity distributions applied to aquatic risk assessment for zinc[J]. Environmental Toxicology and Pharmacology, 2002, 11(3-4): 167-172.

[21] BRATTIN W J, BARRY T M, CHIU N, et al. Monte carlo modeling with uncertain probability density functions[J]. Human and Ecological Risk Assessment: An International Journal, 1996, 2(4): 820-840.

[22] LIU Q, XU X, ZENG J, et al. Development of marine water quality criteria for inorganic mercury in china based on the retrievable toxicity data and a comparison with relevant criteria or guidelines[J]. Ecotoxicology, 2019, 28(4): 412-421.

[23] DING T, DY S, ZHANG Y, et al. Hardness-dependent water quality criteria for cadmium and an ecological risk assessment of the Shaying River Basin, China[J]. Ecotoxicology and environmental safety, 2020, 198: 110666.

[24] 张志霞，王斌，袁宏林，等. 运用物种敏感度分布法推导磺胺类药物的水质基准[J]. 环境科学与技术, 2016, 39(12): 184-188.

[25] BATLEY G E, VAN D R A, WAME M S J, et al. Technical rationale for changes to the method for deriving Australian and New Zealand water quality guideline values for toxicants[R]. Australian Government Standing Council on Environment and Water, Canberra, 2014. 

[26] FISHER R, VAN D R, BATLEY G, et al. Key issues in the derivation of water quality guideline values[R]. Australian Institute of Marine Science, 2019.

[27] MICHAEL W, BATLEY G E, VAN D R A, et al. Revised method for deriving Australian and New Zealand water quality guideline values for toxicants: Prepared for the revision of the Australian and New Zealand guidelines for fresh and marine water quality[R]. Australian Government Department of Agriculture and Water Resources, 2018.