“由于范德瓦尔斯方程只考虑了刚球之间的吸引力， 而未考虑排斥力，所以与实际气体并不十分符合[1]”、“范氏理论在定量上还不能正确地描述临界点附近气体的性质[2]”、“在实际应用中，如果需要较高的精度，即使在较低压强下范德瓦尔斯方程也不适用[3]”。气体如何精确处理？能用简洁的数学方法精确处理范氏方程所存在的缺陷问题吗？

1. 玻尔兹曼因子方法

1.1. 气体平衡体系的表面保守力场与表面自由能

与范德瓦尔斯方程所考虑的原理类同，认为在图1中靠近器壁的ABB’A’区域内存在着垂直于器壁的表面保守力场：在低压强条件下，由于体系内部相邻分子之间的平均间距大于图2中的，相邻分子之间的相互作用合力为引力，故区域的表面保守力场为引力势场；在高压强条件下，由于体系内部相邻分子之间的平均间距小于图2中的，相邻分子之间的相互作用合力为斥力, 故ABB’A’区域的表面保守力场表现为强大的斥力势场.由于体系内部分子溢出ABB’A’区域（节流）过程中，必须克服垂直于器壁的表面保守力做功，所以紧靠容器壁的气体分子都具有可以转变为机械能的表面自由能（表面引力势场中为正, 斥力势场中为负），数值上等于体系内部分子通过表面保守力场溢出体系(节流)过程中所必须做的功。

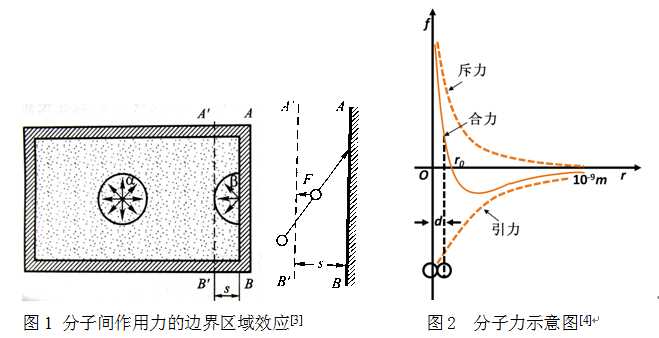
由于图1中(ABB’A’区域)气体表面保守力场所固有的表面自由能既包含气体内部分子之间的引力特性，也包含相邻分子之间的斥力特性，所以采用表面自由能作为统一描述气体内部分子之间相互作用合力特性的状态参量，就既可解决范德瓦尔斯方程因“未考虑排斥力，所以与实际气体并不十分符合”[1]问题，又可巧妙地消弥了“统计物理学处理互作用粒子系统所遇到的困难”问题。

1.2. 玻尔兹曼因子方法

当只是讨论气体平衡体系表面分子在表面保守力场方向上按表面位势能的分布(类似于“重力场中微粒按高度的分布”[3])时，完全可以将气体平衡体系的“表面”，近似理解为是由完全相同的只受表面保守力场作用的“近独立粒子”所组成的热力学系统。根据“玻尔兹曼分布律是一个普遍性的规律，它对任何物质微粒（气体、液体、固体的原子和分子、布朗粒子等）在任何保守力场（重力场、电场）中运动的情形都成立”[3]的科学论断，描述气体平衡体系的物态方程可以由气体表面分子在表面保守力场方向上的分布特性，采用玻尔兹曼统计分布原理获得。

定义：将玻尔兹曼分布律直接应用于气体平衡体系表面保守力场中，用表面保守力场所固有的表面自由能作为描述体系内部分子之间相互作用合力特性的状态参量，并由此推导出气体物态方程的方法，称之为玻尔兹曼因子方法。

2.实际气体的玻尔兹曼因子方程

“内涵决定表面，表面反映内涵[5]”。若从表面(ABB’A’区域)入手，应用玻尔兹曼因子方法，就可以推导出纯理论的物态方程—实际气体的玻尔兹曼因子方程[6]：

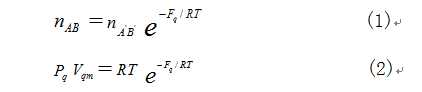
实际气体的玻尔兹曼因子方程(式2)不仅函盖、超越了理想气体物态方程、范德瓦尔斯方程与昂内斯的维里方程，而且在可实验实测的宏观特性参量P_q ，V_qm ，T与不可实验实测的微观特性参量—摩尔表面自由能F_q 之间架起了衔接的桥梁，为精确计算摩尔表面自由能F_q 及其相关的物理量打开了方便之门，实现了精确处理气体平衡体系的目标。换言之，由玻尔兹曼因子方法推导出来的实际气体的玻尔兹曼因子方程，与热力学基础知识一脉相承，不仅能百分之百地替代理想气体物态方程、范德瓦尔斯方程与维里方程，说明它们所能说明的科学现象，而且可以准确地说明它们不能解释的科学现象。例如(详见参考文献[6]第4章)

(1)用简洁的数学语言准确地描述气体临界系数、焦耳―汤姆逊效应等基础物理概念；

(2)在定量上准确描述气体在各种压强条件下的自然状态，彻底地解决了范氏方程‘在实际应用中，如果需要较高的精度，即使在较低压强下范氏方程也不适用的缺陷问题；

(3)应用实际气体的玻尔兹曼因子方程可以推导出摩尔气体定压热容CPqm与定容热容CVqm之差的理论公式3表明:摩尔实际气体定压热容CPqm与定容热容CVqm之差，不仅只是与压缩功R 直接相关，而且是玻尔兹曼因子指数-Fq /RT的函数，是一个与分子平均间距(即摩尔体积)直接相关的物理量。应用式2、3，可以直接计算摩尔实际气体定压热容与定容热容之差、之比，且对多种气体进行定量计算的理论结果，都与实验观测值高度吻合[6]。

实际气体的玻尔兹曼因子方程在丰富、完善热力学基础知识方面意义深远，在工程技术领域的实际应用前景广阔。

3. 小结

“内涵在表面上，是一种存在的现实，也是一种关于世界的常识性的认知[7]。”应用玻尔兹曼因子方法,从气体平衡体系的“表面（或界面）”入手，由表及里，用气体平衡体系表面保守力场所固有的表面自由能，作为统一描述气体内部分子之间相互作用合力特性(既含引力特性，也含斥力特性)的状态参量，就可以解决古老的气体如何精确处理问题，就能够用简洁的数学语言，消弥范氏方程所存在的缺陷问题。

参考文献

[1]  汤文辉, 张若棋. 物态方程理论及计算概论 ( 笫 2版 ) [M ]. 北京: 高等教育出版社, 2008第二版 47页.

[2]  梁希侠、班士良  统计热力学 第2版[M]（北京：科学出版社）2008. 241、242页

[3]  钱尚武，章立源，李椿 热学(第2版)[M]。北京：高等教育出版社，2008. 72页

[4]  张三慧  大学物理学 热学、光学学、量子物理学[M]  第3版（北京清华大学出版社）2009.28页

[5]  罗会仟 爱刷脸的物理世界 科学网博客 2016.06.01

[6]  吴义彬  边缘奇迹:玻尔兹曼因子方法开启了准确计算物质特性的大门  南昌 江西科学技术出版社，2016.9. 16～18、22～38页. 

[7] 曹则贤  现代物理知识  2012.01.012