我按参考文献[1]提出的机理作进一步定量计算时发现,所能传出的角动量要比太阳必须传出的角动量小了3个数量级,故只得放弃这种解释而另找起因。我假设这种分布格局是在星云塌缩过程中造成的;然后对该 过程进行了详细定量的理论分析计算,发现参考文献[1]所提出的角动量转移的机理在此期间就已存在,而且向外所转移的角动量比星云盘演化期大很多个数量级,这正好圆满地解释了现在“分布异常“的起因。我已就此撰写了题为《太阳系角动量分布异常起因的定量新解释》的论文;但因其篇幅超过9千字,不便投送本栏目,我已将它登录在我的博客上。现根据该文观点对原始太阳星云(以下简称“星云”)塌缩过程作如下扼要的介绍;读者感兴趣的话,其详情可在网上搜索“赵菊初的博客”即可查阅。
1、星云有关起始参数的确定
1.1 主流观点初步认定的参数
认为星云大致呈球形,直径约为3000~10000AU(AU为天文单位);质量为1.001~1.1个太阳质量之间;其温度约为10~100K;密度为10-20~10-8g/cm3,折算为10-17~10-5kg/m3。
其中有些参数还未获得最终确认,还有待进一步核实。
1、2待定参数的确定
1.2.1 星云自转角速度的设定
主流观点认为,星云是上一代恒星爆炸的产物,故其角动量也应来自它。按已知参数算出太阳绕银河系公转的角动量为:9.72×1055kg·m2/s;它比太阳自转角动量约大14个数量级。假设这一比值也适用于上一代恒星,那么可以认为,星云的角动量仅取决于上一代恒星绕银河系公转的角动量,因此,其中一部分转变成太阳星云后,各质点仍应保持相同的角速度,这时,整个星云将绕银河系中心作同步自转;按其公转周期为2.5亿年可算出其角速度ω0=7.97×10-16s-1。
1.2.2 星云总质量及总角动量的设定
按1.1节取其折中值,即取星云总质量等于1.01个太阳质量,约为2×1030kg。
现在还未发现星云演化时,角动量大量逃离太阳系的证据和机理,故仍设它大体等于现在太阳系的总角动量。
1.2.3 星云密度分布规律及其直径的计算
假设星云密度自中心向外按线性规律递减,外径处的密度ρ1=10-16kg/m3,则密度分布规律可用下式表示:

根据边界条件:r=0,M=0可得C=0。
1.2.4 单位体积星云物质所受各种力的计算
(1) 单位体积星云物质所受引力的计算
牛顿曾经证明,我也可以证明,对于密度只随半径而改变的星体,在其内部以其质心为中心的任意球面上的重力加速度,将与球面以内的物质质量成正比,与球面半径r的平方成反比,球面以外的质量对球面上任一点的引力合力将等于零。故星云中任意点单位体积星云物质所受引力可按下式计算:
式中负号是考虑F定义为正值而加入的。由上式可算得在r=R处:F2=-5.54×10-33sin2θN。
(3) 单位体积星云物质所受压差力的计算
这里省略其计算及推导过程,直接列出:在r=R处:F3=-1.36×10-20N。
2、探寻星云塌缩时角动量转移的机理
如果星云在塌缩时不存在角动量转移,那么,由于F比F2及F3大14个数量及以上,所以在引力F的主导作用下,星云全部角动量都将集中分布在塌缩后形成的原始太阳上。由于角动量的转移量等于相互作用的力矩与作用时间的乘积,如果塌缩时间很短,就无法完成大量角动量的转移,因此又需先计算星云各层位完成塌缩过程的时间,然后再探讨星云内部物质角动量轴向转移的机理。
2.1星云各层位塌缩时间的计算
星云外径塌缩时间的计算公式可由以下积分方程解出:

(1) 式中的动力粘度η可按参考文献[1]

中的(9)式计算;它是麦克斯韦从纯理论基础上推导出来的并为后来的实验所证实,这被认为是分子运动理论的光辉成就之一。 据报导,在宇宙空间99%以上的物质都以等离子态存在;氢离子可看作质子,其质量约为氢分子质量的一半;其直径约为1.6~1.7×10
-15m;约等于1.6~1.7×10
-5埃;它比氢分子直径 约小5个数量级。若取星云塌缩时的温度为500K,则可算出η≈2.02×10
5Pa·s;该粘度值如此之大,若不是按经典公式算出真使人不敢相信;而它正好是星云角动量大量转移的关键因素所在。上式中的比值(r/r
0)可根据时间t试算求出,Δt为总塌缩时间t按n等分后的等分值。
按上式用数值积分法求得的半径为r0的球面上输出的总角动量J及参照参考文献[2]算出的该球面内星云物质原来具有的总角动量J1列于表1。
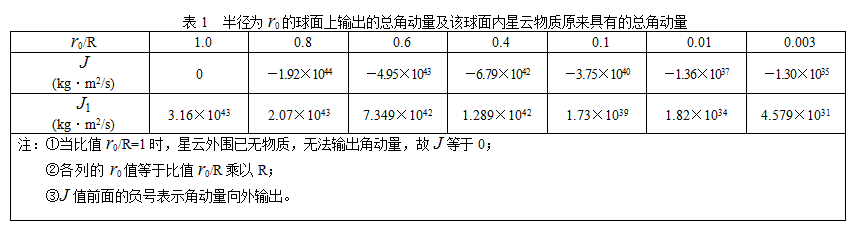
由上表可以看出,星云在塌缩期足以将绝大部分角动量转移给外围的星云盘,而形成现在太阳系角动量分布的格局。由于篇幅所限,交待不清之处,如比值Δr0/Δr的计算等,可从“博客”中查阅。
参考文献:
[1] 赵菊初,太阳系角动量分布异常的起因探讨,中科院科学智慧火花栏目,2012-02-19
[2] 赵菊初,地球转动惯量的计算,中科院科学智慧火花栏目,2012.11.6

