一、四色定理

每幅㊣ (每一国连成一片,两国共同边界是条线而非有限的点,无一国包围其它国家,至多三国相遇一点)最多需要四种色能使相邻国着不同色.

它从1852年问世至今尚未获得数学证明.

符号含意:㊣正规地图,☆五构形,※PC被E分隔、PA相邻、CA不相邻,△根据归纳假设,□四色定理成立,⊙不妨视,P-1P着色1或着色是1.

二、定理 定义 引理

肯普定理:每幅㊣至少有一国有二、三、四或五个邻国,无每一国都大于五个邻国的情形.

按此㊣可分为二构形、…、☆四种情形.

定义：

1-对各种构形,称邻国数最少的国家为构形国.

2-约定㊣所有国家连成一片内部无空区域,并称内部和外部的界线（简单闭曲线）为㊣边界.

3-国B一段边界在㊣边界上,则称B为边沿国.

4-一些国家包围了其它国家,则称这些国家形成的环为圈.

引理1:☆的国家数的集W＝｛12,14,15,…,n,…｝.

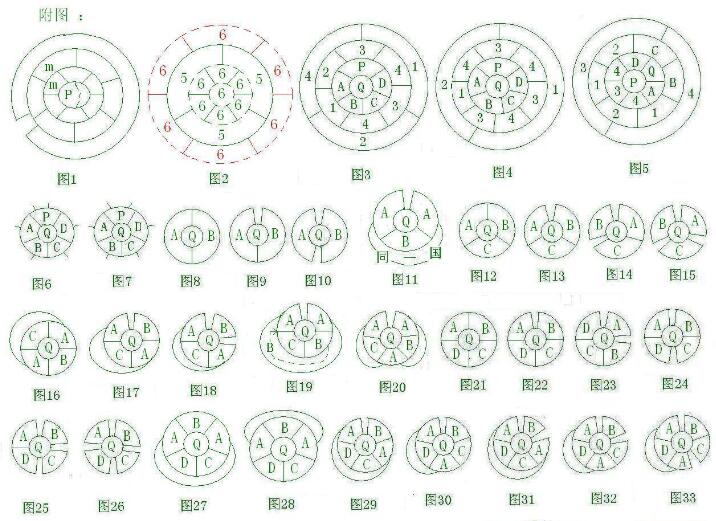
证:构造无穷多“四圈”☆.类似图1的☆,内外圈各一国,中间两圈上取数列6,7,…,m,…（m≥6）⑴中的同一项,得国家数由大于12的偶数组成数列14,…,2（m+1）,…⑵；虚线将P分成两国,得国家数由大于13的奇数组成数列15,…,2m+3,…⑶. 易验证1-13中 仅12有☆.合并数列⑵⑶及12得到所有☆的国家数的集W=｛12,14,15,…,n,…｝.

除12外W中每个n所对应☆不同结构的个数复杂程度无论如何,皆视为由“四圈”☆演变而成.

引理2:任意☆中存在构形国不是边沿国.

证:假设命题不成立,则有一个☆G,使得构形国都是边沿国.因平面地图与球面地图等价,故可使G的以边沿国形成的圈T在球面上并把球面分成对称的两部分.令每部分被T包围的国家S对称地布满,示意如图2.由此知T上每一国的邻国数（原来不一定都是五）都大于七,其余国家的邻国数都大于五,就得到一幅（STS）每一国的邻国数都大于五的㊣.这与肯普定理矛盾,故G不存在.证毕.

引理3:在n≥15的☆中,若包围构形国Q的每个邻国与Q只有一条共同边界,Q的邻国两两相邻的组数是五,这五个邻国中存在邻国数大于五的国P,则□.

证:若☆每一国的邻国数都是五,则n=12.由类似图1的结构知n≥15时,每个n至少与一个“四圈”☆对应,故完全具备引理3的条件.

⑴n=15时,只有图3-5三种情形,图中国家数由内到外各依次为1563、1572及1662.图3,QP都具备引理3的条件.视AQ为E,B（P）由五（六）个邻国变成四（五）个,其余国家的邻国数未变,☆变成四构形；至多用四种色,使得四构形在不相邻的PC（※）着同色时相邻国家能着不同色,如P-1C-1E-3B-2D-2（1-2-3-4为色码,不会混淆）,其余国家着色如图,□；把Q换成色4,则□.图4,视AQ为E,BP都由六个邻国变成五个,其余国家的邻国数未变,还是☆；至多用四种色,使得☆在不相邻的PC（※）着同色时相邻国家能着不同色,如P-1C-1E-3B-2D-2,其余国家着色如图,□；把Q换成色4,则□（E的邻国数是六.图5类似可证）.

⑵假设15≤n≤k时□,图6,视PAQBCD依次着色是134212,即是说QP都具备引理3的条件,假设都是按上述模式操作的方法着色,视AQ为E,PEBCD依次着色是13212,显然BPE的邻国数分别不小于四五六,其余国家的邻国数未变,国家数满足14≤n≤k-1,除14外的每个n值,都含有A和Q合并前与后两种情况,前为☆后为四构形或☆.至多用四种色,使得每个n值所对应的四构形或☆在不相邻的PC（※）着同色时相邻国家能着不同色,⊙P-1C-1E-3B-2D-2（若BD异色,则与归纳假设相悖.如B-4,由n=k-1〔AQ合并后〕时□,但不能还原n=k时□）,即□（换色前）.把Q换成色4,□.

n=k+1时,图7,取一个具备引理3条件的构形国Q,视AQD为E,则 E的邻国数大于六,PBC的邻国数都不小于四.其余国家的邻国数未变,n=k-1（合并后）,其构形为四构形或☆.根据换色前的归纳假设,即…在不相邻的PC（※）着同色时相邻国家能着不同色,⊙P-1C-1E-3B-2,□（换色前）.把Q换成色4,□.证毕.

三、证明四色定理

证：1≤n≤15时已公认□.

假设15≤n≤k时□；

n=k+1时,令Q为构形国,分类论证如下.

㈠二构形

图8-11,视AQ为E,则n=k.△,□,⊙E-1B-2.把Q换成色3,□.

㈡三构形

1Q的每个邻国与Q 只有一条共同边界

图12,视AQ为E,则n=k.△,□,⊙E-1B-2C-3.因EBC只用了三种色着色,且Q被ABC包围,故Q能换成色4,□.

图13-15,视AQ为E,则n=k.△,□.因（Q是边沿国）BC至多用了两种色着色,故Q至少能换成第四色,□.

2Q的邻国中至少有一国与Q至少有两条共同边界

图16（不能有两个圈）-20,A与Q至少有两条共同边界.同图13的证明.

㈢四构形

1Q的每个邻国与Q只有一条共同边界

图21-26,视AQC为E（显然AC及BD中至少有一组不相邻,在图21-22中⊙AC不相邻）,则n=k-1.△,□.因EBD至多用了三种色着色（BD相邻为异色）,故Q至少能换成第四色,□.

2Q的邻国中至少有一国与Q至少有两条共同边界

这时若有Q的邻国AB分别与Q形成圈T和H,显然H在T内或外且互不干扰.即使有Q的两个邻国与Q形成圈S,S也在T内或外,故只需考虑一组T即可.当T或（可兼）S型圈超过一组时,均未也不必画出相应的图,如图19.☆也如此不再述.

T的个数是1,图27-34,因四构形每一国的邻国数都大于三,故T至少包围了两国（非下确界）.视T包围的国家为E,则n≤k,△,□,⊙A-1Q-2.因T外部至少有Q的一个邻国,去掉T外部的国家,则n≤k,△,□；因AQ只用了两种色,故总可使得A-1Q-2.把前次T及其外部的着色部分与后次T内部的着色部分拼成原来的四构形,□.图35,AC相邻时,A、Q与C形成两个圈,取一个圈仿图27的证明易证□；不相邻时,视AQC为E,同图22的证明（此法仅适于T及S型圈）.

T的个数大于1,图36-39,任取一个圈,按图27的证明（后次要去掉该圈外A的一部分）,再把所需的两部分拼成原来的四构形,□.

㈣五构形

由引理2可令Q不是边沿国.

1Q的每个邻国与Q只有一条共同边界

⑴Q的邻国中没有两国与Q形成圈

①Q的邻国中每一国的邻国数都是五

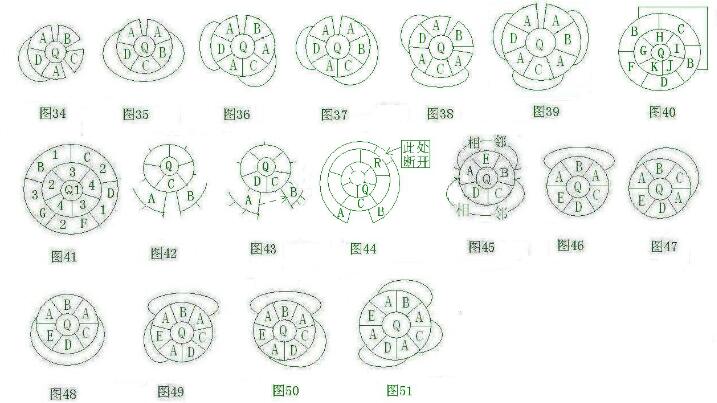
ⅰQ的邻国无边沿国,则Q的邻国被四国BCBDF或五国BCDFG形成的圈包围.图40,视BGHIJKQ为E,则n=k-5.△,□,⊙E-1D-2F-3C-2或4.把GHIJKQ重新着色成434312或232314,□.图41,视Q及邻国为E,则n=k-4.△,□,⊙圈上着色是12123,E-4.把E的六国重新着色,如图□.

ⅱQ的邻国有边沿国

Q的邻国有边沿国的位置只有一处

与某边沿处邻近的两国只有两种情形.图42, 若AB不是同一国,不相邻时,把AB拓展成相邻（不影响其它国家的相邻关系,下同此）并视为E,仿图8的证明易证□,再收缩成原状,□；相邻时,⊙C不是边沿国（在此处把AB拓展成相邻）,这时Q的邻国无边沿国,变为情形ⅰ已证.再收缩成原状,□.若AB是同一国, 则AC形成的圈T至少包围了五国.T外部至少有一国时,仿图27的证明易证□.T外部无国家时, 至少有一非Q的邻国R与AB相邻,示意如图44.否则☆只有7国,这与n＞15矛盾.把AB拓展成Q的邻国无边沿国而又在某处断开,使得无一国包围其它国家且R成为边沿国,就变成情形ⅰ,已证.再还原成原状, □.

图43, 若AB不是同一国,AB不相邻时,把A按箭头方向拓展成与B相邻并视为E,按图42“AB不相邻”的情形证明;AB相邻时,把A按箭头方向拓展成与B“相邻”,则C有六个邻国.此时同“②Q的邻国中每一国的邻国数不都是五”情形的证明. 再收缩成原状,□.若AB是同一国,拓展A使图43成为图42,按图42“AB是同一国”的情形证明.

Q的邻国有边沿国的位置至少有两处

图42-43,这时显然AB不是同一国也不相邻,仿图42“AB不是同一国,不相邻时”的情形易证明□.

②Q的邻国中每一国的邻国数不都是五

此即Q的邻国中存在邻国数大于五的国家,对此引理3已证明n≥15时□.故此时□.

⑵Q的邻国中有两国与Q形成圈

图45,AQB形成一个（两种情形）或两个圈,取一个圈仿图27的证明易证□.

2Q的邻国中至少有一国与Q至少有两条共同边界

图46-51,AQ形成一个至三个圈,取一个圈仿图27或36的证明易证□.证毕.

参考文献:

R.柯朗（美国）著,《数学是什么》.