1、高次纵横图的提出。

如果一个n阶纵横图，其每一个数的k次幂仍是一个纵横图，那么将这样的纵横图称为n阶k次纵横图，当k＞1时，即称其为高次纵横图。其实，不管是低次纵横图还是高次纵横图，乃至其它各种类型的纵横图，它们最初都是作为数字游戏硬凑出来的。由于现在可以运用计算机去硬凑，所以现在各种类型的纵横图极其丰富多彩。

据说2次纵横图是弗洛劳夫（Frolow）在1892年首先发现，立即引起了许多数学家的注意。随后的赖利（Rilly）则花了九年时间，不仅给出了200多个此类二次纵横图，并且还证明了，这样的二次纵横图决不会低于八阶。然而，赖利似乎并未证明，所有的二次纵横图，必定同时也是偶数阶的传统纵横图，也就是它们全都具有这样的双重特性。

现在有人在二次纵横图的基础上，又进一步发展出了三次纵横图。原先认为三次纵横图的阶数不可能低于64，但是后来有人陆续做出了32、16阶的三次纵横图。德国人特鲁姆泼（Trump）于2002年，首先做出了一个12阶的三次纵横图。几乎同时，我国的高治源和潘凤雏于2003年2月，一下子就拿出了二个12阶的三次纵横图。这些三次纵横图全都具有三重特性，它们既是一个三次纵横图，又是一个二次纵横图，同时也是一个一次偶数阶的传统型纵横图。

如果n阶r次纵横图存在，那么，它是不是都会具有上述这样的r重特性？其最小的阶数又会是一个什么样的数？特别是其每一行的n个数，是不是都是由n/2个和为n²+1的组对数所构成？它们的列是不是全部都是两两对应，相互两两结成n个和为n²+1的数对？对于这些问题，只能通过自然数的等幂和予以解答。因此，高次纵横图的出现，实际上反映了以往大家对于自然数的等幂和的研究，实在太肤浅了，迫使我们不得不重新给予更为深入的研究。

2、从杨辉的垛积术到朱世杰的逐差法。

如果说杨辉的纵横图，是对于中国纵横图的杰出贡献，那么杨辉的垛积术，则完全是他的独立创造。有人说杨辉的垛积术，是对于沈括隙积术的发展，这是不对的，因为垛积术与隙积术，是性质完全不同的二类数学问题，根本不能将它们混为一谈。沈括的隙积术，是一个将离散问题，转化为连续问题去予以解决的数学。

杨辉的垛积术，则是一个反复离散的问题，由此引发出了差分的问题，差分具有与微分相类似的性质。杨辉将自然数的平方和称为四隅垛，他将其分拆成一个1阶等差级数，和二个2阶等差级数分别进行计算，给出了下面的四隅垛计算公式。我国宋末元初时期的朱世杰，发展了杨辉的垛积术，他将自然数的三次方之和分拆成一个等差级数，六个2阶等差级数，六个3阶等差级数分别进行计算。

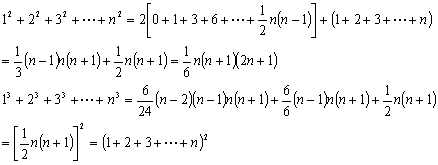
朱世杰的这个公式，是运用了他所首创的“逐差法”而得到。微积分的创始人莱布尼茨，则比朱世杰晚了三百多年，也推导出了这个公式。莱布尼茨是西方数学家里少有的正人君子，如果他的这个公式是抄袭了别人，他不会不予以说明。其实，朱世杰的“逐差法”，实际上已经解决了自然数的任意次等幂之和的问题。

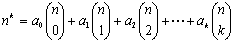
“逐差法”的实质内容，是如何将n^k拆分为上面n的k次多项式，其中的系数a _r（r=0，1，2，…，k），则是n^k的各阶差分的首项数，因此这些系数都是一些正负交错的多项式。其中的组合符号 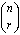，则是一个n项的r阶等差级数的和，也是一个r+1阶等差级数的第n项数，即最后一项数。

其实，对于我国古代的“周易三角”——二项式（1+1）ⁿ的展开式来说，当n是奇数时，其 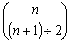的右上角数列，是一个标准的（n-1）/2阶等差数列。其 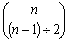的右上角数列，是一个标准的（n-3）/2阶等差数列。……其 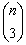的右上角数列，是一个标准的2阶等差数列。其 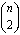的右上角数列，是一个标准的1阶等差数列。所谓标准等差数列，是指公差为1的1阶等差数列。当n是偶数时，具有完全类似的规律。

3、李善兰数列与欧拉数列。

根据朱世杰的“逐差法”，应该不难给出全体自然数，k次幂和的统一的计算公式。或许朱世杰当时认为，没有必要再作进一步的汇总，或许朱世杰当时没有找到，恰当的表达方式，因此这个统一的计算公式直到道光年间，才由清代著名数学大师李善兰给出如下：

对于这个递归数列，李善兰还具体给出了一个，被称为“乘方垛各廉表”的递归数表。此表运用Lm k的上标m=0，1，2，…表示m乘方垛的乘方次数，即横行序数；下标k=0，1，2，…，m为项数。李善兰的“乘方垛各廉表”，具有以下三个重要特性：第一是边界性，即有L0 0=1和Lm m=1；第二是对称性，即有Lm k=Lm m-k；第三是倍积性，即有

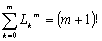
李善兰的这个运用数列所表示的统一公式，极其晦涩难懂，必须具备乘方垛方面的丰富知识，才能明白其中的道理。其实，这个统一公式的最大的缺点是不便实际应用，尽管这个统一公式还可以运用三角数表予以表示，然而还是无法展开对于高次纵横图的研究。无独有偶的是，西方《近代组合学》里的欧拉数列A（n，k），居然与我国的李善兰数列完全相同。尽管他们所运用的方法完全不同，然而他们的推导，似乎更其晦涩难懂。

我国从朱世杰的“逐差法”，到李善兰的递归数列，却经历了三个朝代五百多年时间。然而西方数学从莱布尼茨到欧拉，只有短短几十年时间。这是因为此时的中国数学，由于儒家数术的恶性发展，已经濒临中断的境地。然而此时的西方数学，才摆脱宗教的黑暗压制不久，完全处于突飞猛进的上升时期。

4、自然数等幂和的解析表达。

笔者在研究高次纵横图的多重性及其择阶性时，意外发现了自然数等幂和的解析表达式。正是由于这个发现了，才是使得对于高次纵横图的探究得以深入下去。其实，这个解析表达式，也是进一步探索高阶等差数列，以及高阶差分多项式的关键。对于自然数等幂和自身来说，也只能通过这个解析表达式去认识。

运用朱世杰的“逐差法”，对于n的k次幂n^k解析分拆，其中的道理比较晦涩难懂，确实不易解释清楚，让人难以理解透彻。然而，下面对于n的k次幂n^k解析分拆，则是换了一个角度的重新思考，从而使得问题变得十分直观清晰，非常简单易懂了。当然，这两种方法是完全相通的。

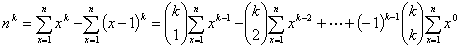
此式将n的k次幂n^k分拆为k个正负相间的项，每项则是自然数的k-r（r=1，2，…，k）次等幂之和，分别与（1-1）^k的展开项，除了第一项以外的各项反号之积。按照同样的方法，即可给出（n-1）^k，（n-2）^k，……，2 ^k，1^k的表达式如下，尽管它们仍是k个正负相间的项，每项仍是一个k-r（r=1，2，…，k）次等幂之和，然而其中的自然数则是逐个减少。

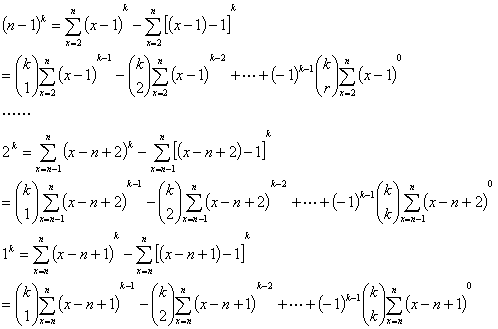
上面的各式相加，即得全体自然数等幂之和的解析表达式，显然，这个解析表达式是其全体低次幂和的组合。由此即可证明高次纵横图的多重性，因此，一个k次纵横图，必定也是一个k-1，k-2，……，2，1次纵横图。由于一个k阶等差数列，加减一个低阶等差数列之后，仍是一个k阶等差数列。由于一个k阶等差数列，与任何一个正整数的积，仍是一个k阶等差数列。

所以自然数的k-r（r=1，2，…，k）次等幂，是一个k+1阶等差数列，这就是说，一个k次纵横图，必定也是一个k+1阶等差数列。为了能将一个k次n阶顺序图的组对差调整为0，这个n最小得是2^k+1。然而，3次12阶纵横图却是存在的，其实这是一个唯一的例外，因为只有全体自然数的三次等幂之和，还可以运用平方和的方法去予以表示。