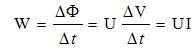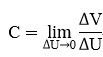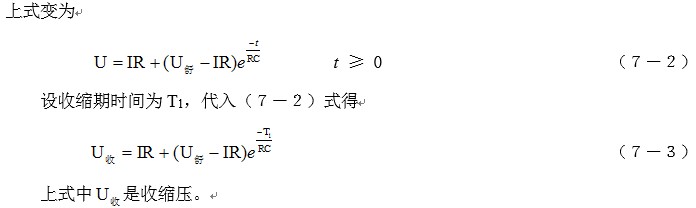1.1 液阻
设血压为U,血流量为I,约定:
U = IR
其中R为新定义的参量,该约定即为其定义式。R可以称为液阻,这一概念和电阻类似。
1.2 液容
根据热力学理论,体积变化时所做的功为
ΔΦ =UΔV
其中ΔΦ为所做的功,U为压强,ΔV为体积变化量,设时间为Δt,则功率
血流量的输出功率与心脏的功能有关,血流量I的大小也和心脏的功能有一定关系。
定义:
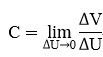
C可称为液容。对于局部组织间隙(包括血管),液体的容积增量V与液体的静压增量U的比值即为液容(平均值)。所以:
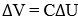
。
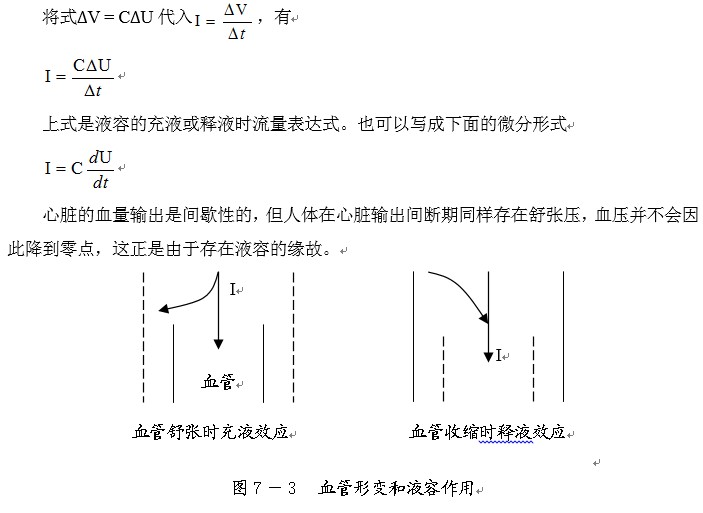
显然,当局部组织的液体静压U升高时,液体的容积V也随之升高。譬如,当组织液静压升高时必然使组织液容量增加,组织液因此滞留。液容C是一个普遍存在的参量,不仅组织间隙,血管也同样存在液容。由于存在液容,当血压升高时,血管将扩张,血管内血液的容量将增加,这是一个血管充血液过程;当血压降低时,血管收缩,血管内血液的容量将减少,这是血管释放血液的过程。
2.1 血压分析
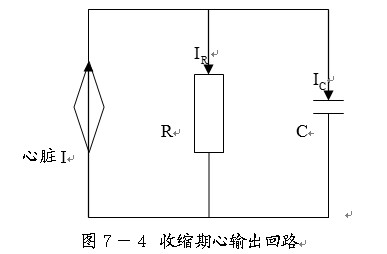
2.1.1 收缩期回路
血压能影响血管扩张,影响组织液静压,影响血液循环和组织液回流,影响细胞氧化代谢强度,并能影响局部组织增生。不同的疾病有不同的血压变化特征,并且血压是能直接测量的物理量,所以深入分析血压变化特点很有必要。
任何一段血管都可以看成是血流液阻和液容的并联。
下图是心脏收缩期回路简单模拟,血管的状态用R和C简单并联表示。由于血管各处都存在液容,实际的情况可能很复杂,但用简单参数分析,也同样能反映血液循环的一些特性。为了分析的方便,将心脏射血输出量近似为恒流源。
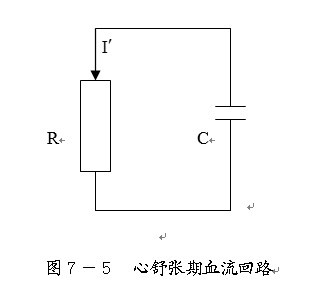
2.1.2 舒张期回路
接下来看看舒张期情况。下图是舒张期回路,储存在液容(血管)中的血液将通过回路释放。
2.1.3 整个心动周期分析
设心脏的工作状态非常稳定,心动周期为T = T1 + T2,则根据(7-3)式和(7-6)式,有